Генеральная и выборочная дисперсия

Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику - генеральную дисперсию.

Генеральной дисперсией 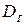называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

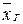Если все значения 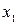, ,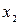..., 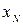признака генеральной совокупности объема N различны, то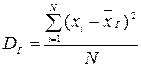

Если же значения признака 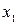, ,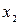..., 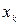имеют соответственно частоты 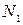, ,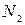..., , 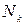причем 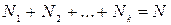, то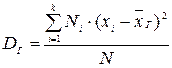

Пример 1. Генеральная совокупность задана таблицей распределения:

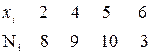
Найти генеральную дисперсию.

Решение: Найдем генеральную среднюю:

.

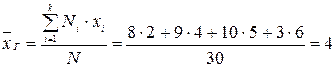Найдем генеральную дисперсию:

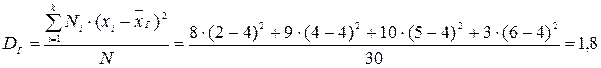
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: .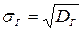

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 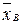вводят сводную характеристику - выборочную дисперсию.

Выборочной дисперсией 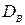называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

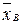Если все значения 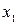, ,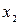..., 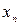признака выборки объема n различны, то

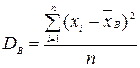
Если же значения признака 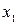, ,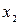..., 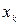имеют соответственно частоты 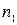, ,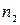..., , 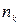причем 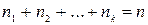, то .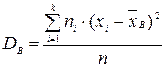

Пример 2. Выборочная совокупность задана таблицей распределения:

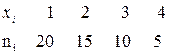
Найти выборочную дисперсию.

Решение: Найдем выборочную среднюю:

.

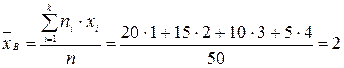Найдем выборочную дисперсию:

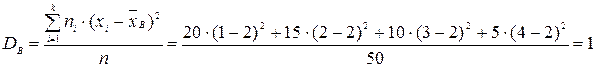
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: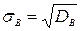

Вычисление дисперсии, безразлично - выборочной или генеральной, можно упростить, используя следующую теорему.

Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней: .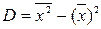

Пример. Найти выборочную дисперсию по данному распределению

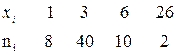
Решение. Найдем выборочную среднюю:

.

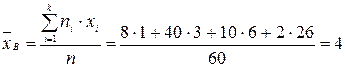Найдем среднюю квадратов значений признака:

.

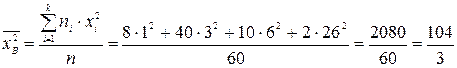Искомая дисперсия: .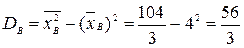

Пусть нам необходимо по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию 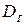. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой 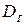другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно .

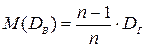Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить 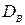на дробь 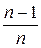. Сделав это, получим исправленную дисперсию, которую обычно обозначают через :

.

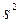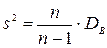Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии.

Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию .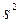

Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:

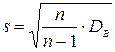
17.5 Точность оценки, надёжность. Доверительный интервал

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, - точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже).

Пусть найденная по данным выборки статистическая характеристика 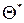служит оценкой неизвестного параметра 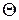. Будем считать 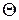постоянным числом (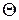может быть и случайной величиной). Ясно, что 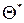тем точнее определяет параметр 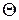, чем меньше абсолютная величина разности . Другими словами, если и , то чем меньше , тем оценка точнее. Таким образом, положительное число характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка 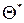удовлетворяет неравенству ; можно лишь говорить о вероятности 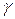, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки 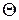по 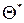называют вероятность 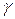с которой осуществляется неравенство . Обычно надежность оценки задается наперед, причем в качестве 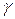берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что , равна : .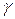

Заменив неравенство равносильным ему двойным неравенством , или , имеем

.

Это соотношение следует понимать так: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметр 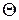, равна .

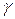Доверительным называют интервал , который покрывает неизвестный параметр с заданной надежностью .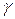

Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Дата добавления: 2014-01-06