Доверительные интервалы для оценки математического ожидания нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней 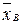. Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью .

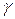Примем без доказательства, что если случайная величина X распределена нормально, то выборочная средняя 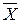, найденная по независимым наблюдениям, также распределена нормально. Параметры распределения 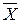таковы: ,

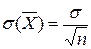
Потребуем, чтобы выполнялось соотношени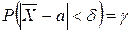е , где 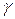- заданная надежность.

,

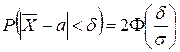, где .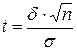

Найдя из последнего равенства , можем написать

.

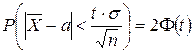Приняв во внимание, что вероятность Р задана и равна 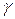, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через )

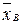Смысл полученного соотношения таков: с надежностью 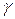можно утверждать, что доверительный интервал 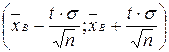покрывает неизвестный параметр а; точность оценки .

Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства 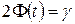, или ; по таблице функции Лапласа (см. приложение 2) находят аргумент t, которому соответствует значение функции Лапласа, равное .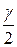

Пример 1. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением 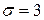. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним 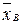, если объем выборки n=36 и задана надежность оценки 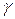=0,95.

Решение: Найдем t. Из соотношения 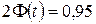получим . По таблице приложения 2 находим t=1,96.

Найдем точность оценки: .

Доверительный интервал таков: (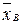- 0,98; 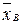+ 0,98). Например, если 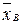=4,1, то доверительный интервал имеет следующие доверительные границы:

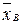-0,98=4,1—0,98=3,12; 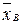+0,98=4,1+0,98=5,08.

Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12< а <5,08.

Если среднее квадратическое отклонение неизвестно то доверительный интервал для оценки математического ожидания нормального распределения имеет вид: , покрывающий неизвестный параметр а с надежностью .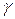

По таблице приложения 3 по заданным n и 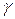можно найти .

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=16 найдены выборочная средняя 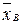=20,2 и «исправленное» среднее квадратическое откло­нение s=0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение: Найдем . Пользуясь таблицей приложения 3, по 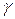=0,95 и n=16 находим =2,13.

Найдем доверительные границы:

.

.

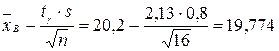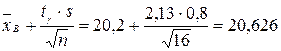Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774< а <20,626.

17.7 Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение по «исправленному» выборочному среднему квадратическому отклонению s. Доверительные интервалы, покрывающие параметр с заданной надежностью 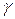таковы:

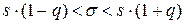, если q<1.

, если q>1.

Для отыскания параметра q пользуются таблицей приложения 4.

Пример 1. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=25 найдено «исправленное» среднее квадратическое отклонение s=0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,95.

Решение. По таблице приложения 4 по данным 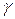=0,95 и n=25 найдем q=0,32. Т.к. q<1, то для вычисления доверительного интервала применяем первую формулу

Искомый доверительный интервал таков:

0,8 (1-0,32)< <0,8 (1+0,32), или 0,544< <1,056.

Дата добавления: 2014-01-06