Боковые реакции на колесах в процессе поворота

При движении автомобиля на поворотах большое значение имеет распределение поперечных реакций между колесами переднего и заднего моста.

Для определения поперечных реакций, возникающих на колесах передней (R_у1) и задней оси (R_у2), составим уравнение моментов сил относительно центра масс автомобиля по рис. 60:

Рис. 60. Схема сил и моментов при повороте автомобиля

Боковые реакции уравновешивают поперечную составляющую силы инерции, поэтому:

R_x1sinθ + P_jу = R_у1cosθ + R_у2. (233)

Криволинейное движение автомобиля можно рассматривать как процесс его вращения вокруг вертикальной оси, проходящей через центр тяжести. При этом уравнение вращения имеет следующий вид:

J_z(dω/dτ) = (R_у1cosθ - R_x1sinθ)а - R_у2b - M_соп2, (234)

где J_z - момент инерции автомобиля относительно вертикальной оси, проходящей через центр тяжести автомобиля.

Решая (220) и (221) совместно, получим формулы боковых реакций:

R_у1 = 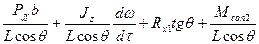; (235)

R_у2 = 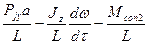. (236)

Величина угловой скорости вращения автомобиля вокруг оси равна величине угловой скорости поворота автомобиля вокруг мгновенного центра вращения. Найдем значение углового ускорения:

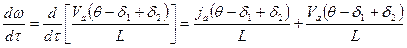. (237)

Момент инерции автомобиля относительно вертикальной оси выразим через его массу и радиус инерции (ρ_z):

J_z ~ M_aρ_z². (238)

Во многих случаях можно принять ρ_z² ≈ ab. Подставляя выражения (237) и (238) в ранее полученные формулы (235) и (236), после соответствующих преобразований получим:

R_у1 = 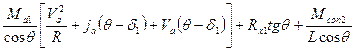; (239)

R_у2 == 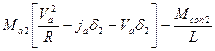. (240)

В формулах (239) и (240) первые члены (содержащие квадратные скобки) выражают не что иное, как реакцию опорной поверхности на действие сил инерции. При этом инерционная составляющая R_у1 и R_у2 имеет решающее значение, и лишь при малых скоростях движения значение боковых реакций определяют продольные реакции на передних колесах (R_x1) и момент сопротивления повороту, создаваемый задними колесами (M_соп2). Для случая установившегося кругового движения при небольшом угле поворота управляемых колес (cosθ ≈ 1) и малом сопротивлении опорной поверхности (R_x1 ≈ 0), а также отсутствии значительного момента сопротивления повороту, создаваемого задними колесами (M_соп2 ≈ 0), формулы боковых реакций приобретают самый простой вид:

R_у1≈ 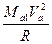; (241)

R_у2 ≈ . (242)

Как следует из формул (241) и (242), величины боковых реакций, прикладываемых к колесам передней и задней оси, прямо пропорциональны массам (M_a1 и M_a2), приходящимся на соответствующие оси. Углы увода δ₁ и δ₂ запишутся:

δ₁ = Р_у1/к_ув1 =М_а1V_а²/(к_ув1R); (243)

δ₂ = Р_у2/к_ув2 =М_а2V_а²/(к_ув2R). (244)

Разность углов дает следующее выражение:

δ₂ - δ₁ = 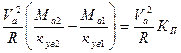, (245)

где К_п – коэффициент поварачиваемости.

Если К_п > 0 - избыточная поварачиваемость, К_п = 0 - нейтральная поварачиваемость, К_п < 0 - недостаточная поварачиваемость.

Дата добавления: 2014-01-06