Тема 4. Решение антагонистической игры с седловой точкой

Рассмотрим проблему выбора игроками эффективных стратегий в антагонистической игре с несколько иных позиций.

Для лучшего обозрения сведем рассмотренные действия игроков A и В в соответствующие таблицы.

Действия игрока А Действия игрока В

№ хода	Выбранная стратегия	Выигрыш		№ хода	Выбранная стратегия	Выигрыш
		–
...	…	...		...	...	...

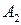
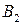
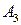
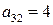
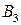
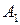
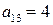
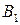
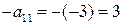
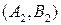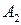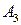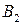Из этих таблиц видно, что после первых ходов игроков А и В сложилась ситуация , которая устраивает игрока В (он получает максимальный выигрыш), но не устраивает игрока А (он получает минимальный "выигрыш" ). Поэтому игрок А своим вторым ходом, меняя стратегию на , приводит игру к ситуации , которую уже не приемлет игрок В. Игрок В заменяет стратегию на 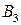и исходом игры становится ситуация и т. д. Смена ситуаций выглядит следующим образом:

Таким образом, ситуации, складывающиеся после очередных ходов игроков, являются неустойчивыми.

Однако свойство неустойчивости ситуаций присуще не каждой игре. В этом можно убедиться на следующем примере.

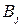
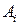
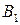
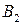
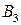
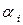
					(4.1)
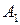
	0,7	0,5	0,3	0,3
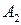
	0,6	0,9	0,4	0,4
	0,7	0,9	0,4	0,4   0,4

В данном случае максиминной стратегией игрока А является стратегия 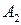, а минимаксной стратегией игрока В - стратегия .

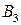Если игрок А придерживается своей максиминной стратегии 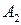, то игрок В должен выбрать свою минимаксную 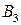с тем, чтобы выигрыш игрока А (или, что то же, проигрыш игрока В) был минимальным (во 2-й строке матрицы (4.1)). На это игрок А должен ответить выбором опять же стратегии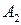, чтобы получить максимальный (в 3-м столбце) выигрыш . Ответным ходом игрок В опять выбирает стратегию 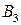и т. д.

Таким образом, если игроки А и В придерживаются своих максиминной и минимаксной стратегий соответственно, то ни один из них не может увеличить свой выигрыш, отступая от своей стратегии. Ситуация (А₂, В₃) является в дайной игре устойчивой.

Нижняя и верхняя цены игры совпадают:

Пример показывает, что существуют игры, нижняя цена которых равна верхней, т.е., и в которых ситуации минимаксных стратегий обладают свойством устойчивости. В основе теоретического анализа таких игр лежит ряд понятий. Приведем соответствующие определения.

Пусть имеем -игру, игроки А и В которой обладают соответственно следующими множествами чистых стратегий: 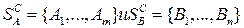. Пусть матрица этой игры имеет вид (5.12).

Ситуация 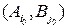(сложившаяся в результате выбора игроками А и В соответственно стратегий,) называется удовлетворительной (приемлемой, допустимой) для игрока А, если

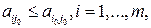(4.2)

и у довлетворительной для игрока В, если

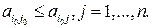(4.3)

Ситуация 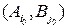называется равновесной, или ситуацией равновесия, или устойчивой, или седловой, точкой игры, если она удовлетворительна для каждого из игроков А и В, т.е. если выполняются неравенства (4.2) и (4.3):

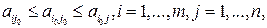
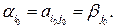
Выигрыш 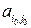, соответствующий ситуации равновесия 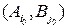, называют седловой точкой матрицы игры. Таким образом, элемент 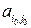, являющийся седловой точкой матрицы игры, является минимальным в своей 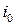-й строке и максимальным в своем -м столбце. Игра, матрица которой содержит хотя бы один такой элемент, называется игрой с седловой точкой.

Теорема 6.5. Для того чтобы существовала цена игры в чистых стратегиях, т.е. для того чтобы нижняя цена игры 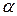равнялась верхней цене игры 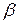, необходимо и достаточно существование у матрицы этой игры седловой точки.

Соотношения между множествами оптимальных стратегий каждого игрока, с одной стороны, и множествами максиминных стратегий игрока А и минимаксных стратегий игрока В, с другой стороны, устанавливается следующей теоремой.

Теорема 6.6. Справедливы следующие утверждения.

1. Каждая оптимальная стратегия игрока А является его максиминной стратегией, а каждая оптимальная стратегия игрока В является его минимаксной стратегией.

2. В игре без седловых точек ни одна из максиминных и минимаксных стратегий не является оптимальной, поскольку в этой игре вообще нет оптимальных стратегий.

Дата добавления: 2014-01-06