Тема 7. Решение игры в смешанных стратегиях

Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение

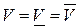
называется ценой игры в смешанных стратегиях, а стратегии и для которых выполняются равенства

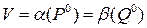
(и тогда это общее значение равно ), называются оптимальными смешанными стратегиями соответственно игроков А и В.

Таким образом, оптимальные смешанные стратегии и (которые, в частности, могут быть и чистыми) обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.

Нетрудно показать, что

т. е. цена игры в смешанных стратегиях V не меньше нижней цены игры в чистых стратегиях а и не больше верхней цены игры в чистых стратегиях.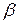

Полным решение игры в смешанных стратегиях называется совокупность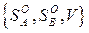множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий и цена игры V образуют частное решение в смешанных стратегиях.

Основная теорема теории игр, сформулированная и доказанная фон Нейманом¹, устанавливает существование решения любой конечной матричной игры.

Теорема 7.1 (основная теорема матричных игр фон Неймана). Любая матричная игра имеет решение в смешанных стратегиях, т. е. существуют цена игры в смешанных стратегиях V и оптимальные смешанные стратегии и соответственно игроков А и В, т. е.

Теорема 7.2 (свойство равнозначности седловых точек). Если и 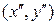- седловые точки функции 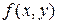на декартовом произведении , то значения данной функции в этих точках совпадают:

Теорема 7.3 (критерий существования седловой точки). Для того чтобы функция 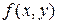, , , имела седловую точку на декартовом произведении , необходимо и достаточно, чтобы существовали

и

и выполнялось их равенство

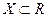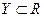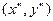Пример 7.1. Пусть и , т.е. х и у - скалярные переменные, и точки и , которые графически изображаются двумя вершинами прямоугольника (см. рис. 7.1), являются седловыми точками функции . Тогда по свойству взаимозаменяемости, сформулированному в теореме 9.3, остальные две вершины этого прямоугольника 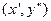и также являются седловыми. В связи с этим иногда свойство взаимозаменяемости седловых точек называют свойством "прямоугольности".

Если, в частности, , то точки , 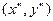лежат на одной вертикали , а если , то эти точки лежат на одной горизонтали ; поэтому в этих случаях взаимозамена неравных координат этих точек приводит к паре тех же точек и прямоугольник вырождается в отрезок.

Рис. 7.1

Пример 9.3. Применяя критерий (теорема 9.4), определить, существует ли у функции

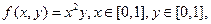
на декартовом квадрате [0,1]² седловые точки.

Решение. Очевидно, что

при любом ,

и, следовательно,

Также очевидно, что

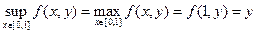, при любом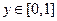

и потому

.

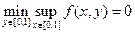Итак, имеем

т.е. выполняются необходимые условия и потому на квадрате [0,1]² существуют седловые точки.

Дата добавления: 2014-01-06