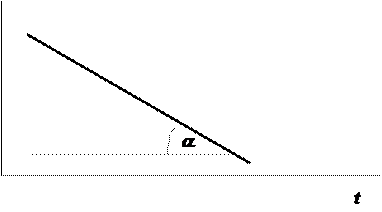Реакции первого порядка

Для произвольной реакции 1-го порядка вида

А ® продукты реакции

уравнение закона действующих масс выглядит так:

d С v = - ¾¾ = kC, d t

где С - концентрация вещества А. После разделения переменных

d С k d t = - ¾¾ C

это уравнение можно интегрировать в интервалах = 0 ¸ t, и С ₀ ¸ С_t:

t C_t d С k ò d t = - ò ¾¾, 0 C₀ C

получая при этом

k (t - t₀) = - (ln C_t - ln C₀)

или

k (t - t₀) = ln C₀ - ln C_t,

откуда, принимая t₀ = 0, получаем окончательное кинетическое уравнение для расчёта константы скорости реакции первого порядка:

1 С₀ k = ¾ ln ¾¾. (12.4) t C_t

где С₀ - начальная концентрация исходного вещества; C_t - концентрация, измеренная в момент времени t.

Из этого уравнения следует, что константу скорости реакции 1-го порядка можно определить графически, если построить график зависимости
ln С от времени. При этом тангенс угла наклона графика равен - k (рис. 12.2).

Строя график зависимости ln С от t для неизвестной реакции и получая при этом прямую линию, подобную изображённой на рис. 12.2, можно убедиться в том, что реакция имеет первый порядок.

Константа скорости может быть определена и без построения графика, а именно, как среднее арифметическое из величин, полученных при расчёте по уравнению (12.4) для нескольких текущих концентраций исходного вещества, экспериментально измеренных в различные моменты времени.

Так как в уравнение (12.4) входит отношение начальной и текущей концентраций, то в принципе оно может быть заменено отношением любых

	ln С

Рис. 12.2. Зависимость ln С - t для реакции первого порядка

других величин, пропорциональных концентрации (например, уг­лов вращения плоскости поляризации реакционной смеси или её оптической плотности и т. п.), а сама концентрация может быть выражена любыми способами. Часто при вычислениях используют не концентрацию, а количество вещества в молях. Тогда расчётное уравнение для константы скорости будет выглядеть так:

1 а k = ¾ ln ¾¾¾, (12.5) t а- х

где а - начальное число молей исходного вещества, x - число молей его, прореагировавшее к моменту времени t.

С помощью уравнений (12.4) и (12.5) могут быть вычислены (если известна константа скорости) и другие важные кинетические характеристики, например, время полупревращения какой-либо реакции или, что представляет особый интерес для фармации, срок годности лекарственных препаратов.

Время полупревращения (t _1/2) реакции удобно вычислять с помощью преобразованного уравнения (12.5):

1 а t = ¾ ln ¾¾¾. k а - х

Принимая х = а /2, получим:

1 а 1 0,693 t _1/2 = ¾ ln ¾¾¾ = ¾ ln 2 = ¾¾¾, (12.6) k а - а /2 k k

Это же выражение можно получить, используя уравнение (12.4) и принимая C_t = C₀ /2.

Из уравнения (12.6) следует, что время полупревращения реакции первого порядкане зависит от начальной концентрации вещества. То есть для уменьшения концентрации, например, от 1 до 0,5 М потребуется ровно столько же времени, сколько для уменьшения концентрации от 0,001 до 0,0005 М. Из уравнения (12.6) следует также, что по экспериментально найденному значению t _1/2 можно вычислить константу скорости реакции:

0,693 k = ¾¾¾. t _1/2

Реакции разложения многих лекарственных веществ, особенно реакции, идущие в растворах, являются реакциями первого или псевдопервого порядка, поэтому срок годности их тоже может быть рассчитан по кинетическому уравнению (12.5). Согласно действующей нормативной документации лекарственный препарат считается годным к употреблению, если содержание лекарственного вещества в нём отвечает требованиям соответствующей фармакопейной статьи. Принимая, что в свежеприготовленном препарате количество наиболее быстро разлагающегося вещества а = 100%, а допустимый процент разложения лекарственного вещества равен х, можно, зная константу скорости разложения данного вещества при температуре его хранения, по уравнению

1 100 t = ¾ ln ¾¾¾¾. k 100 - х

вычислить ориентировочный срок его годности.

Дата добавления: 2014-01-06