Пример. Можно ли такой ожидаемый результат рассматривать как приемлемый для инвестора?

Инвестиции в 100 тыс. руб. с равной вероятностью могут принести доход либо в 200 тыс. руб., либо нулевой доход. Тогда ожидаемый доход от инвестиций равен:

200∙0,5 + 0∙0,5 = 100 тыс. руб.

Можно ли такой ожидаемый результат рассматривать как приемлемый для инвестора?

Ответ на вопрос не в последнюю очередь зависит от его финансового положения. Если 100 тыс. руб. - это вся сумма, которой располагает инвестор, то скорее всего рассчитанный результат для него не подходит: потенциальный риск потерять всю сумму денег не компенсируется адекватным потенциальным вознаграждением - получением в случае успеха 200 тыс. руб. Напротив, если инвестор располагает большим капиталом, например, в 1 млн. руб., то риск для него может оказаться приемлемым. Таким образом, индивидуальная полезность одной и той же суммы денег (100 тыс. руб.) не одинакова для первого и второго инвесторов. Для второго лица она меньше, поэтому оно готово рискнуть, несмотря на возможность потерять деньги.

Поскольку результат от владения активом точно не определен, то, принимая решение о его покупке, «обходимо учитывать как возможный доход, так и риск неполучения этого дохода. В связи с этим в качестве аргументов функции ожидаемой полезности следует рассматривать ожидаемый доход (богатство) и риск неполучения данного дохода. Как было показано в приведенном выше примере, принятие инвестиционного решения зависело не только от абсолютной величины ожидаемого результата, но и его возможной дисперсии, т.е. риска неполучения положительного результата.

Всех инвесторов можно разделить на три группы:

Инвестор считается не склонным к риску, если из двух активов с одинаковой ожидаемой доходностью, но разным риском, он выберет менее рискованный актив, т.е. актив с меньшей дисперсией результатов.

В финансовой теории полагается, что большинство инвесторов не склонны к риску. Это, однако, не означает, что они не готовы идти на более высокий риск. Это говорит лишь о том, что в случае увеличения риска актива качестве потенциальной компенсации они требуют и более высокой ожидаемой доходности с его стороны.

Инвестор считается склонным к риску, если из двух активов с одинаков ожидаемой доходностью, но разным риском, он выберет более рискованный актив, т.е. актив с большей дисперсией результатов. Такой инвестор предпочитает рискнуть в надежде получить более высокую доходность в случае благоприятного исхода, однако может понести и потери при неблагоприятном развитии событий. Он рассчитывает получить дополнительную полезность от дополнительного риска.

Инвестор считается нейтральным к риску, если он не учитывает его при принятии инвестиционных решений. Это означает, что инвестор безразличен в выборе между двумя активами с одинаковой ожидаемой доходностью, но раз ным риском. Как правило, инвесторы нейтральны к риску для его небольших значений.

Переформулируем приведенные определения с использованием понятий функций полезности и ожидаемой полезности. Инвестор является не склонным к риску, если значение функции полезности от получаемой суммы денег равной ожидаемому доходу, больше значения функции полезности от покупки актива. Инвестор склонен к риску, если значение функции полезности от получаемой суммы денег равной ожидаемому доходу актива меньше значения функции ожидаемой полезности от покупки актива. Если оба значения для него одинаковы, то он нейтрален к риску.

Пусть некоторый актив S может приносить только два результата – доход а с вероятностью р и доход b с вероятностью (1- р). Тогда ожидаемый доход актива E(S) составляет:

E(S) = ap + b(1-p)

Величина полезности, получаемая инвестором как функция от гарантированной суммы равной ожидаемому доходу актива, равна:

,

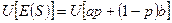Значение ожидаемой полезности рискованного актива, на которое инвестор ориентируется при принятии решения о его покупке, определяется как средневзвешенная полезность каждого из возможных фактических результатов. Весами выступают вероятности исходов

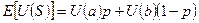
Функция является линейной комбинацией полезностей U(a) и U(b) для разных значений вероятности исхода. Поэтому графически она представляет прямую, соединяющую эти точки.

Выше мы определили, что инвестор не склонен к риску, если

>

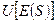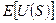
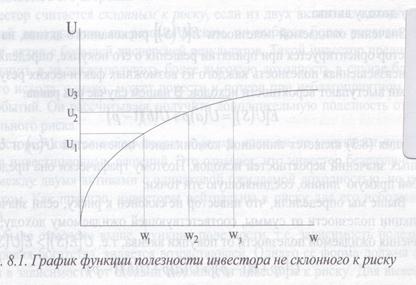w – богатство

Как видно из графика, по мере роста богатства инвестора растет и его общая полезность, однако дополнительная, или предельная, полезность богатства уменьшается. Это означает, что функция его предельной полезности является убывающей. Не склонный к риску инвестор при утрате части богатства теряет больше полезности, чем получает ее при росте богатства на такую же величину. Поэтому среди рискованных активов с одинаковым уровнем ожидаемой доходности он всегда выберет менее рисковый.

Для инвестора склонного к риску величина полезности получаемого дохода равному ожидаемому доходу актива меньше величины ожидаемой полезности от покупки актива, т.е.

<

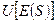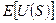
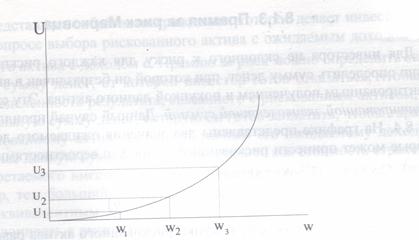Из графика видно, что предельная полезность богатства возрастает по мере роста богатства. При этом по мере роста богатства на одну и ту же величину, полезность увеличивается в большей степени при сравнении с ее уменьшением на ту же величину. В результате среди активов с одинаковыми ожидаемыми доходностями, о разным риском инвестор предпочтет более рисковый актив.

Для инвестора нейтрального к риску характерно равенство значений

=

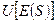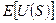
Для него величина предельной полезности остается неизменной при изменении богатства.

3 Премия за риск Марковица

Для инвестора не склонного к риску для каждого рискованного актива можно определить сумму денег, при которой он безразличен в выборе между ее гарантированным получением и покупкой данного актива. Эту сумму называют гарантированной эквивалентной суммой.

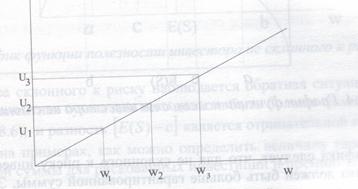
На графике представлены два значения ожидаемого дохода - а и b, которые может принести рискованный актив S с вероятностями исходов - р и (l - р). Ожидаемый доход актива составляет:

E(s) = ap + b(1-p)

Ожидаемая полезность от покупки рискованного актива равна E[U(S)]. На рис. 8.4 ее значение найдем, опустив перпендикуляр из точки е на ось ординат. Не склонный к риску инвестор не будет покупать данный актив, поскольку полезность от получения гарантированной суммы E(S) согласно графику составляет 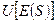и она больше величины 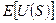. В то же время на графике функции полезности существует точка g, соответствующая доходу с, в которой полезность инвестора такая же как и в точке е. Это говорит о том, что с точки зрения полезности инвестор безразличен в выборе между гарантированным получением суммы с и покупкой рискованного актива с ожидаемым доходом E(S) Уровень дохода с является эквивалентным гарантированным доходом, соответствующим ожидаемому доходу E(S).

U[E(S)] E[U(S)] U(a)

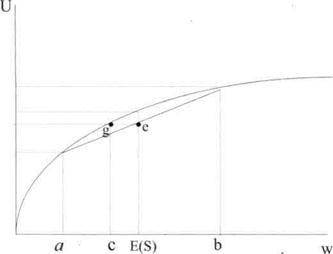
График функции полезности инвестора не склонного к риску

Из графика следует, что для не склонного к риску инвестора ожидаемый доход актива должен быть больше гарантированной суммы. Эту разность именуют премией за риск Марковица. На рис. 8.4 ее величина равна E(S) - c.

Премия за риск представляет собой вознаграждение, которое делает инвестора безразличным в вопросе выбора рискованного актива с ожидаемым доходом e(s) или безрискового актива с доходом с.

Премию за риск можно определить как ту максимальную сумму денег, от которой инвестор готов отказаться, чтобы исключить неопределенность результата, связанного с рискованным активом, или как ту максимальную сумму денег, которую он готов заплатить, чтобы гарантировать по рискованному активу результат равный его ожидаемому доходу. В последнем случае данную сумму удобно представить как стоимость страховой полиса, приобретаемого вместе с рискованным активом. Чем менее склонен к риску инвестор, тем больший ожидаемый доход должен предлагать актив по сравнению с эквивалентным доходом.

Для не склонного к риску инвестора разность [E(S) - с] >0.

На основе сказанного можно сделать вывод о том, что не склонный к риску инвестор выберет рискованный актив, если премия за риск для него больше премии за риск Марковица и актив без риска, если она меньше. При равенстве данных величин оба актива для него являются одинаковыми.

Для инвестора склонного к риску наблюдается обратная ситуация. Гарантированная эквивалентная сумма для него должна быть больше ожидаемого дохода и разность [E(S)-с] <0. Рассмотрим на примерах, как можно определить величину гарантированной эквивалентной суммы для рискованных инвестиций и премию за риск Марковица.

Дата добавления: 2014-01-06