Общий случай движения твёрдого тела

Покажем, что любое движение твёрдого тела можно представить как сумму двух его движений: поступательного и вращательного.

Пусть тело движется произвольным образом. Выделим произвольную точку. Этой точкой может быть какая-либо точка твёрдого тела или точка пространства. Назовём эту точку полюсом. Обозначим – скорость полюса относительно неподвижной системы координат XYZ. Запишем для полюса и каждой точки тела тождества:

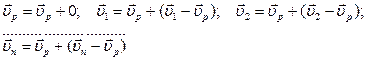
Рассматривая эти тождества, мы видим, что движение твёрдого тела можно представить в виде суммы двух движений: В первом движении все точки тела имеют одну и ту же скорость. Следовательно, первое движение есть поступательное движение АТТ со скоростью полюса, во втором движении у всех точек твёрдого тела, кроме полюса, скорость не равна нулю. Следовательно, второе движение есть вращение тела вокруг полюса. Можно показать, что угловая скорость вращения вокруг полюса не зависит от выбора полюса. Таким образом, можно сделать вывод: любое движение абсолютно твёрдого тела можно представить как сумму двух его движений: поступательного со скоростью полюса и вращательного движения вокруг полюса с угловой скоростью, не зависящей от выбора полюса.

Можно показать, что скорость любой точки тела относительно неподвижной системы координат равна:

, (2.20)

где 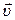– скорость точки твёрдого тела относительно неподвижной системы координат; – скорость полюса относительно неподвижной системы координат; – угловая скорость вращения тела относительно полюса; – радиус-вектор, задающий положение в неподвижной системе координат точки, скорость которой ; – радиус-вектор, задающий положение полюса в неподвижной системе координат;

, (2.21)

где – ускорение точки твёрдого тела относительно неподвижной системы координат; – ускорение полюса относительно неподвижной системы координат; 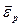– угловое ускорение вращения тела относительно полюса.

Дата добавления: 2014-01-06