
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Самый правый интеграл в формуле (4.3) называется трехкратным интегралом по области V
|
|
|
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Василевский А.И. История менеджмента. Курс лекций. РУДН. humanities.edu.ru.
2. Виханский О.С., Наумов А.И. Менеджмент. М. Гардарики, 1999.
3. Дафт Р.Л. Менеджмент. СПб. Питер, 2002.
4. Дуборкина И.А. Учебный план и программа курса «Менеджмент». М. АО «Диалог-МГУ», 1997.
5. Иванов И.А. Инновационный менеджмент. Ростов-на-Дону. Баро-пресс, 2001.
6. Игнатьева А.В. Исследование систем управления. М. Юнити-Дана, 2002.
7. Кабушкин Н.И. Основы менеджмента. М. ТОО «Остожье», 1999.
8. Классики менеджмента. Под ред. М. Уорнера. СПб. Питер, 2001.
9. Кныш М.И., Пучков В.В., Тютиков Ю.П. Стратегическое управление корпорациями. СПб.: КультИнформПресс. 2002.
10. Кравченко А.И. История менеджмента. М. Академический проект, 2000.
11. Мескон М., Альберт М., Хедоури Ф. Основы менеджмента. М. Дело, 1992.
12. Мишин В.М. Исследование систем управления. М. Финстатинформ, 1998.
13. Попов Е.В. Реинжиниринг бизнес-процессов. М.: 1999.
14. Робсон М., Уллах Ф. Реинжиниринг бизнес-процессов. М.: 1999.
15. Фатхутдинов Р. Инновационный менеджмент. М 1998.
16. Хаммер М. Реинжиниринг бизнес-процессов. М.: 2000.
17. Хотинская Г.И. Финансовый менеджмент. М.: ДИС. 2003.
18. Цыпкин Ю.А. Управление персоналом. М.: Юнити-Дана, 2001.
Если проекция V на 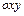 является правильной в направлении
является правильной в направлении 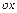 (см. раздел 3.2), то левое равенство в формуле (4.3) остается в силе и мы получим трехкратный интеграл, соответствующий соотношению (3.18).
(см. раздел 3.2), то левое равенство в формуле (4.3) остается в силе и мы получим трехкратный интеграл, соответствующий соотношению (3.18).
Пример 4.1. Вычислить  где V – шар
где V – шар 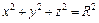 .
.
Поскольку проекция шара на 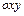 – круг
– круг 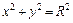 , то получим:
, то получим:
 .
.
Вычислим внутренний интеграл, считая 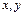 постоянными:
постоянными:

Затем, считая  постоянным, вычислим:
постоянным, вычислим:

где  Поскольку
Поскольку

(см. раздел (1.5), то

Теперь найдем J:

Пример 4.2. Найти с помощью тройного интеграла объем шара 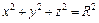 .
.
Поскольку 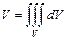 , то, проделав все выкладки предыдущего примера, с той лишь разницей, что здесь
, то, проделав все выкладки предыдущего примера, с той лишь разницей, что здесь  а не
а не 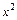 , получим известную формулу
, получим известную формулу 
 Введем понятие цилиндрической системы координат. Для этого рассмотрим в декартовой системе координат точку
Введем понятие цилиндрической системы координат. Для этого рассмотрим в декартовой системе координат точку 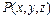 и ее проекцию М на плоскость
и ее проекцию М на плоскость 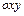 (рис. 4.2). Положение Р вполне определяется полярными координатами
(рис. 4.2). Положение Р вполне определяется полярными координатами  точки М в плоскости
точки М в плоскости 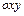 и аппликатой
и аппликатой  . Указанные величины
. Указанные величины  называются цилиндрическими координатами точки М, причем ее декартовы координаты
называются цилиндрическими координатами точки М, причем ее декартовы координаты  связаны с цилиндрическими
связаны с цилиндрическими
 соотношениями:
соотношениями:
 (4.4)
(4.4)
Если проекцией тела V на плоскость 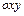 является область S, правильная в полярных координатах (см. раздел 3.3), то из формул (4.3), (3.19) и (4.4) можно получить выражение для тройного интеграла в цилиндрической системе координат:
является область S, правильная в полярных координатах (см. раздел 3.3), то из формул (4.3), (3.19) и (4.4) можно получить выражение для тройного интеграла в цилиндрической системе координат:
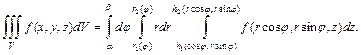 (4.5)
(4.5)
 Пример 4.3. Найти массу М прямого кругового цилиндра высотой h и радиуса R, если его плотность
Пример 4.3. Найти массу М прямого кругового цилиндра высотой h и радиуса R, если его плотность  равна квадрату
равна квадрату  расстояния
расстояния  от точки
от точки 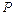 до его оси.
до его оси.
Рассмотрим цилиндрическую систему координат, выбрав начало оси  в центре основания цилиндра, а саму ось направив вдоль оси цилиндра (рис.4.3). Тогда
в центре основания цилиндра, а саму ось направив вдоль оси цилиндра (рис.4.3). Тогда  и для массы М, согласно (4.5) получим
и для массы М, согласно (4.5) получим

Если тело с плотностью  занимает область V, то для координат его центра тяжести
занимает область V, то для координат его центра тяжести 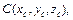 а также моментов инерции
а также моментов инерции 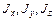 относительно декартовых осей
относительно декартовых осей  справедливы формулы
справедливы формулы
 (4.6)
(4.6)
где 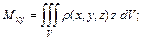

 статические моменты относительно координатных плоскостей;
статические моменты относительно координатных плоскостей;

 (4.7)
(4.7)

4.2. Криволинейный интеграл и его вычисление
Определение. Если каждой точке  области S плоскости
области S плоскости 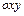 поставлен в соответствие вектор
поставлен в соответствие вектор 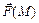 , то говорят, что в области S задано векторное поле
, то говорят, что в области S задано векторное поле 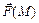 или
или 
Проекциями вектора (вектор-функции)  на оси координат являются функции
на оси координат являются функции  и
и 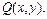 т.е.
т.е.
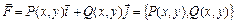
Пусть в области S плоскости oxy задана непрерывная кривая  с началом в точке A и концом в точке B. Пусть в области S также задано векторное поле
с началом в точке A и концом в точке B. Пусть в области S также задано векторное поле 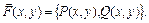
Разобьем кривую  на
на  не обязательно равных частей точками
не обязательно равных частей точками

На каждом участке  выберем по произвольной точке
выберем по произвольной точке  (рис. 4.4) и составим сумму скалярных произведений, называемую интегральной:
(рис. 4.4) и составим сумму скалярных произведений, называемую интегральной:

 (4.8)
(4.8)
при этом  где
где  Дробя кривую
Дробя кривую  на все большее количество участков и стягивая длину
на все большее количество участков и стягивая длину 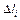 каждого из них к нулю, получим последовательность интегральных сумм
каждого из них к нулю, получим последовательность интегральных сумм 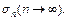
Определение. Если существует предел интегральных сумм  который не зависит ни от способа разбиения
который не зависит ни от способа разбиения  , ни от выбора точек
, ни от выбора точек 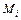 , то этот предел называется криволинейным интегралом от вектор-функции
, то этот предел называется криволинейным интегралом от вектор-функции 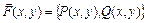 вдоль кривой
вдоль кривой  (дуги AB) в направлении от A к B и обозначается
(дуги AB) в направлении от A к B и обозначается
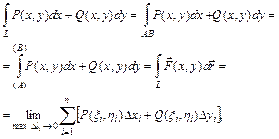 (4.9)
(4.9)
где 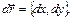 Согласно данному определению, криволинейный интеграл (4.9) равен работе силы
Согласно данному определению, криволинейный интеграл (4.9) равен работе силы  при перемещении вдоль кривой
при перемещении вдоль кривой  от точки A к точке B. Отметим некоторые свойства криволинейного интеграла.
от точки A к точке B. Отметим некоторые свойства криволинейного интеграла.
10. При изменении направления интегрирования вдоль кривой  знак интеграла (4.9) меняется на противоположный
знак интеграла (4.9) меняется на противоположный
 (4.10)
(4.10)
20. Свойство аддитивности (предполагается, что все интегралы существуют):
 (4.11)
(4.11)
Определение. Если кривая  замкнута (т.е. ее начальная и конечная точки совпадают), то интеграл (4.9) называется циркуляцией векторного поля
замкнута (т.е. ее начальная и конечная точки совпадают), то интеграл (4.9) называется циркуляцией векторного поля  по замкнутому контуру
по замкнутому контуру  и обозначается
и обозначается
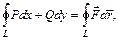 (4.12)
(4.12)
при этом обязательно следует указать направление обхода контура L.
Рассмотрим кривую  (дугу AB), заданную параметрически с помощью функций
(дугу AB), заданную параметрически с помощью функций 
 которые имеют на
которые имеют на  непрерывные производные
непрерывные производные 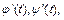 причем значение
причем значение  соответствует точке A, а
соответствует точке A, а  - точке B. Такую кривую будем называть гладкой.
- точке B. Такую кривую будем называть гладкой.
Теорема существования криволинейного интеграла. Для любой вектор-функции  непрерывной вдоль гладкой кривой AB (т.е. при
непрерывной вдоль гладкой кривой AB (т.е. при  и
и  непрерывных вдоль AB) существует криволинейный интеграл (4.9). При этом
непрерывных вдоль AB) существует криволинейный интеграл (4.9). При этом
 (4.13)
(4.13)
Пример 4.4. Вычислить 
где  – верхняя половина эллипса, заданного параметрически:
– верхняя половина эллипса, заданного параметрически:  (t – полярный угол), пробегаемая по ходу часовой стрелки.
(t – полярный угол), пробегаемая по ходу часовой стрелки.
Согласно (4.13) и свойству (4.10) будем иметь


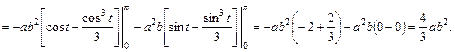
4.3. Формула Грина. Условия независимости криволинейного
интеграла от пути интегрирования.
Первообразная дифференциального выражения.
Пусть границей  области
области 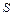 является гладкий замкнутый контур L. Если функции P(x,y), Q(x,y),
является гладкий замкнутый контур L. Если функции P(x,y), Q(x,y), (x,y),
(x,y), 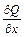 (x,y) непрерывны в
(x,y) непрерывны в  , то справедлива формула Грина:
, то справедлива формула Грина:

 (4.14)
(4.14)
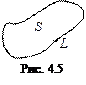 при этом контур L обходится в положительном направлении, т.е. так, чтобы область S оставалась все время слева (рис. 4.5).
при этом контур L обходится в положительном направлении, т.е. так, чтобы область S оставалась все время слева (рис. 4.5).
Пример 4.5. Вычислить J =
где L - окружность  , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
Поскольку
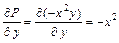 , то согласно (4.14) получим:
, то согласно (4.14) получим:
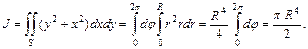
Если в (4.14) принять 
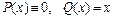 , или же
, или же 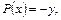
 то получим формулы вычисления площади S фигуры, ограниченной замкнутым контуром L:
то получим формулы вычисления площади S фигуры, ограниченной замкнутым контуром L:
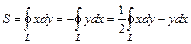 , (4.15)
, (4.15)
при этом обход контура L совершается в положительном направлении.
Пример 4.6. Вычислить площадь, ограниченную эллипсом 

Применяя формулы (4.15) и (4.13) будем иметь

Определение. Если для любых двух точек А и В из области S интеграл 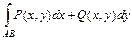 по любому контуру, целиком лежащему в S и соединяющему А и В, принимает одно и то же значение, зависящее только от положения точек А и В, то говорят, что этот интеграл не зависит от пути интегрирования в области S.
по любому контуру, целиком лежащему в S и соединяющему А и В, принимает одно и то же значение, зависящее только от положения точек А и В, то говорят, что этот интеграл не зависит от пути интегрирования в области S.
Теорема. Для того, чтобы

в области S не зависел от пути интегрирования, необходимо и достаточно, чтобы

где Г - любой замкнутый контур, лежащий в S.
Определение. Область S называется односвязной, если для любого замкнутого контура, лежащего в S, ограниченная им часть плоскости целиком содержится в S.
Теорема. Пусть 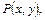 Q(x,y),
Q(x,y), 
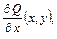 непрерывны в односвязной области S.
непрерывны в односвязной области S.
Тогда для того, чтобы 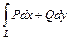 в S не зависел от пути интегрирования необходимо и достаточно, чтобы в S выполнялось соотношение.
в S не зависел от пути интегрирования необходимо и достаточно, чтобы в S выполнялось соотношение.
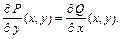 (4.16)
(4.16)
Будем называть выражение 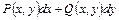 дифференциальным.
дифференциальным.
Теорема. Пусть 

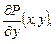
 непрерывны в односвязной области S. Тогда для того чтобы дифференциальное выражение
непрерывны в односвязной области S. Тогда для того чтобы дифференциальное выражение 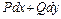 в области S было полным дифференциалом некоторой функции
в области S было полным дифференциалом некоторой функции  т.е.
т.е.  необходимо и достаточно, чтобы в S выполнялось соотношение (4.16)
необходимо и достаточно, чтобы в S выполнялось соотношение (4.16)
Пусть в S задано векторное поле  .
.
Определение. Если функция 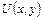 такова, что
такова, что  в S, то она называется первообразной данного дифференциального выражения;
в S, то она называется первообразной данного дифференциального выражения; 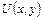 также называется потенциалом векторного поля
также называется потенциалом векторного поля  , а само поле
, а само поле
 - потенциальным.
- потенциальным.
Важно подчеркнуть следующее
(1) Для первообразной U(x, y) выполняются соотношения

 (4.17)
(4.17)
(2) Можно показать, что первообразная 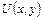 находится по ее дифференциалу с помощью формулы
находится по ее дифференциалу с помощью формулы
 , (4.18)
, (4.18)
при этом начальная точка 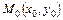 фиксирована, конечная –
фиксирована, конечная – 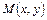 является переменной точкой области S, а сам интеграл не зависит от пути интегрирования от М 0 к М. Переменные интегрирования здесь обозначены через
является переменной точкой области S, а сам интеграл не зависит от пути интегрирования от М 0 к М. Переменные интегрирования здесь обозначены через  , чтобы не спутать их с координатами точки
, чтобы не спутать их с координатами точки 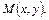
(3) Если  то для любых двух точек
то для любых двух точек 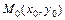 и
и  справедлива формула
справедлива формула
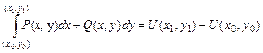 . (4.19)
. (4.19)
Поскольку при заданных начальной 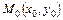 и конечной
и конечной 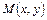 точках для вычисления интеграла (4.18) можно взять любой контур, то выберем в качестве него ломаную
точках для вычисления интеграла (4.18) можно взять любой контур, то выберем в качестве него ломаную 
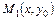 (рис.4.6). Тогда вдоль
(рис.4.6). Тогда вдоль 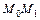 выполняется
выполняется  а вдоль
а вдоль 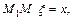

 , откуда, согласно (4.18) будем иметь
, откуда, согласно (4.18) будем иметь
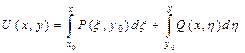 . (4.20)
. (4.20)
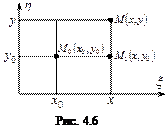
Пример 4.7.
а) найти первообразную  дифференциального выражения
дифференциального выражения 
б) Вычислить интеграл 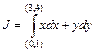
Данное выражение есть полный дифференциал, поскольку 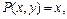
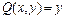 и
и 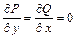 . Зафиксируем некоторую точку
. Зафиксируем некоторую точку 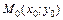 . Тогда, согласно (4.20),
. Тогда, согласно (4.20),
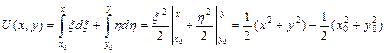 .
.
Если теперь константу  обозначить через с, то мы получим множество всех первообразных:
обозначить через с, то мы получим множество всех первообразных:  .
.
Для того, чтобы посчитать J, воспользуемся формулой (4.19):
 .
.
Глава 5
РЕКОМЕНДУЕМЫЕ ЗАДАЧИ
Раздел содержит некоторые типичные задачи, относящиеся к материалу, изложенному в предыдущих разделах. Сначала представлены общие формулировки этих задач и даны образцы их решений в конкретных примерах. Если задача уже разбиралась ранее, то указывается соответствующая ссылка. Далее следуют варианты заданий для самостоятельного решения, относящиеся ко всем разобранным задачам.
Неопределенный интеграл
5.1. Найти неопределенный интеграл, используя тождественные преобразования подынтегральной функции.
Пример 5.1. Найти: 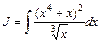


Пример 5.2. Найти: 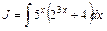

5.2. Найти неопределенный интеграл, пользуясь каким-либо вариантом метода замены переменной.
См. решения примеров 1.4 – 1.7.
5.3. Найти неопределенный интеграл, используя метод интегрирования по частям.
Помимо разобранных здесь примеров, см. также примеры 1.8 – 1.11.
Пример 5.3. Найти: 
Возьмем  ,
,  , откуда
, откуда 
В результате  .
.
Пример 5.4. Найти: 
Сделаем сначала замену переменной 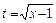 ,
,  , после чего получим:
, после чего получим: 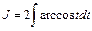 .
.
Далее применим метод интегрирования по частям: возьмем 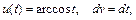 откуда
откуда 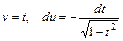 . Таким образом:
. Таким образом:

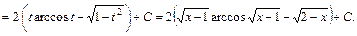
5.4. Найти неопределенный интеграл от выражения, содержащего квадратный трехчлен.
См. решения примеров 1.12 – 1.14.
5.5. Проинтегрировать дробно-рациональную функцию.
См. решения примеров 1.15 – 1.17.
5.6. Проинтегрировать тригонометрическое выражение.
См. примеры 1.19 – 1.24.
Пример 5.5. Найти: 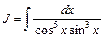

Выбрав  , получим
, получим 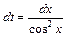 ,
,  , откуда
, откуда


Определенный интеграл
5.7. Вычислить определенный интеграл по формуле Ньютона-Лейбница.
См. примеры 2.2 – 2.6.
5.8. Найти среднее значение функции на заданном отрезке.
Пример 5.6. Найти среднее значение функции 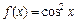 на отрезке
на отрезке .
.
Решение. Согласно определению среднего значения  функции
функции  на отрезке
на отрезке 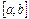 имеем:
имеем:

5.9. Вычислить несобственный интеграл с бесконечными пределами (если он сходится) или установить его расходимость.
Некоторые несобственные интегралы с бесконечными пределами рассмотрены в примерах 2.7 – 2.8.
Пример 5.7. Установить, сходится или расходится интеграл 
Решение:  , но поскольку
, но поскольку  и
и 
 не существует, то
не существует, то  расходится.
расходится.
5.10. Вычислить несобственный интеграл от неограниченной функции на конечном отрезке (если он сходится) или доказать его расходимость.
Материал по данной теме не содержится в предыдущих разделах, поэтому его можно рассматривать как дополнительный. Прежде чем разобрать соответствующие примеры, дадим определения.
Пусть функция  непрерывна на
непрерывна на 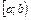 и
и 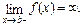 Если существует предел
Если существует предел 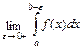 , то он называется сходящимся несобственным интегралом от
, то он называется сходящимся несобственным интегралом от  на
на 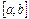 и обозначается
и обозначается  .
.
Если указанного предела не существует, то несобственный интеграл 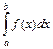 называется расходящимся.
называется расходящимся.
Для случая, когда  непрерывна на
непрерывна на 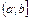 и
и  , несобственный интеграл определяется аналогично:
, несобственный интеграл определяется аналогично:  .
.
Пусть  непрерывна при
непрерывна при  , и имеет в точке
, и имеет в точке 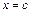 разрыв второго рода. Тогда несобственным интегралом от
разрыв второго рода. Тогда несобственным интегралом от  на
на 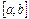 называется
называется

при этом 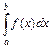 называется сходящимся, если существует каждый из пределов, стоящих справа и расходящимся, если хотя бы один из них не существует.
называется сходящимся, если существует каждый из пределов, стоящих справа и расходящимся, если хотя бы один из них не существует.
Пример 5.8. 

несобственный интеграл расходится.
Пример 5.9. 
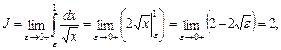
несобственный интеграл сходится и его значение равно двум.
5.11. Приложения определенного интеграла.
Площадь плоской фигуры, длина дуги кривой, объем тела вращения.
См. примеры 2.9, 2.11, 2.15.
Функции нескольких переменных
5.12. Найти частные производные и полный дифференциал функции двух переменных  в заданной точке
в заданной точке 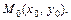
См. примеры 3.3, 3.4.
Пример 5.10. Найти частные производные и полный дифференциал функции  в точке
в точке 
Решение. В произвольной точке  будем иметь
будем иметь 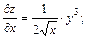

 В заданной точке
В заданной точке 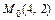 получим:
получим:

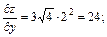
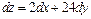 .
.
5.13. Вычислить приближенно заданное выражение.
Пример 5.11. Вычислить приближенно 
Решение. Переведем градусы в радианы:
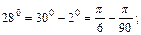
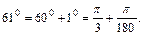
Рассмотрим функцию 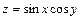 , дифференцируемую в любой точке
, дифференцируемую в любой точке  и вычислим приближенно значение этой функции в точке
и вычислим приближенно значение этой функции в точке

Рассмотрим точку  и примем
и примем  .
.
Поскольку  то
то

Вычислим: 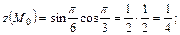
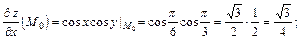
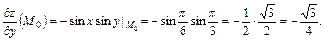
В результате будем иметь:

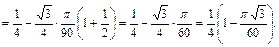
Если принять 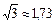 и
и 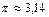 , то
, то 
Двойной интеграл
По данной теме см. примеры 3.5 – 3.10.
5.14. Вычислить двукратный интеграл и представить графически область интегрирования.
Пример 5.12. Вычислить двукратный интеграл  и представить графически область интегрирования
и представить графически область интегрирования
Решение. Область интегрирования 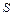 представлена на рис. 5.1
представлена на рис. 5.1



5.15. Переходя к полярным координатам, вычислить заданные двойные интегралы.
См. примеры 3.7, 3.8, 3.9.
5.16. Дать чертеж и вычислить координаты центра тяжести однородной пластины заданной формы.
См. пример 3.10.
5.17. Вычислить моменты инерции однородной пластины заданной формы относительно указанных осей.
 Пример 5.13. Вычислить моменты инерции
Пример 5.13. Вычислить моменты инерции  однородной пластины в форме четверти круга
однородной пластины в форме четверти круга 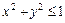 ;
;  относительно осей
относительно осей 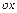 ,
, 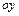 и начала координат.
и начала координат.
Решение. 
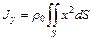 (
(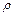 - постоянная плотность пластины). Удобно перейти к полярным координатам
- постоянная плотность пластины). Удобно перейти к полярным координатам 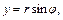
 тогда
тогда
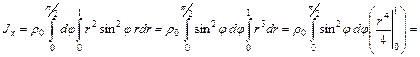
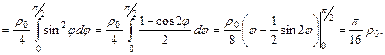
Аналогично  , причем очевидно
, причем очевидно  в силу симметрии пластины относительно прямой
в силу симметрии пластины относительно прямой  . В результате получим
. В результате получим 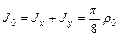 .
.
Криволинейный интеграл
По данной теме см. примеры 4.4 – 4.7.
5.18. Вычислить криволинейный интеграл.
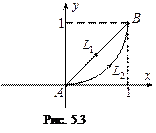 Пример 5.14. Вычислить
Пример 5.14. Вычислить  где
где 
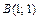 вдоль различных путей
вдоль различных путей 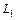 и
и 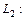
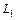 – отрезок прямой
– отрезок прямой 
 – участок
– участок  параболы
параболы 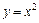
Решение.
1) На пути 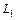
 поэтому:
поэтому:
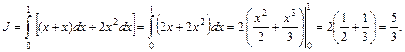
2) На пути 
 поэтому:
поэтому:


5.19. Вычислить криволинейный интеграл от выражения, являющегося полным дифференциалом.
Пример 5.15. Вычислить 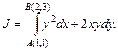
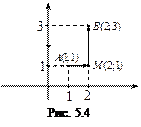 Решение. Подынтегральное выражение действительно представляет собой полный дифференциал, поскольку
Решение. Подынтегральное выражение действительно представляет собой полный дифференциал, поскольку 
 и
и 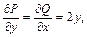 а это значит, что
а это значит, что  не зависит от пути
не зависит от пути  интегрирования, соединяющего точки
интегрирования, соединяющего точки  и
и 
Выбрав в качестве  ломаную
ломаную  где
где 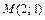 получим
получим

Глава 6
ВАРИАНТЫ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
Неопределенный интеграл
6.1. Найти неопределенный интеграл, используя тождественные преобразования подынтегральной функции.
Вариант 1.
1)  2)
2) 
Вариант 2.
1)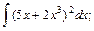 2)
2) 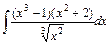
Вариант 3.
1) 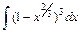 2)
2) 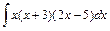
Вариант 4.
1)  2)
2) 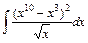
Вариант 5.
1)  2)
2) 
Вариант 6.
1) 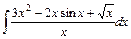 2)
2) 
Вариант 7.
1) 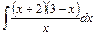 2)
2) 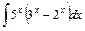
Вариант 8.
1)  2)
2) 
Вариант 9.
1)  2)
2) 
Вариант 10.
1) 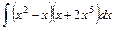 2)
2) 
Вариант 11.
1) 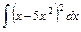 2)
2) 
Вариант 12.
1) 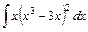 2)
2) 
Вариант 13.
1) 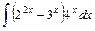 2)
2) 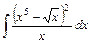
Вариант 14.
1) 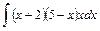 2)
2) 
Вариант 15.
1) 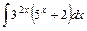 2)
2) 
Вариант 16.
1) 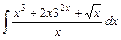 2)
2)
6.2. Найти неопределенный интеграл, пользуясь каким-либо вариантом метода замены переменной.
Вариант 1.
1) 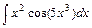 2)
2)  3)
3) 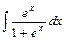
4) 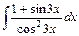 5)
5) 
Вариант 2.
1)  2)
2)  3)
3) 
4)  5)
5) 
Вариант 3.
1) 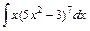 2)
2)  3)
3) 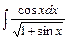
4) 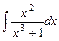 5)
5) 
Вариант 4.
1)  2)
2)  3)
3) 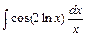
4)  5)
5) 
Вариант 5.
1)  2)
2)  3)
3) 
4) 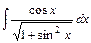 5)
5) 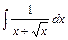
Вариант 6.
1)  2)
2) 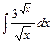 3)
3) 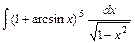
4) 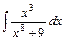 5)
5) 
Вариант 7.
1) 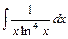 2)
2)  3)
3) 
4) 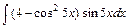 5)
5) 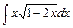
Вариант 8.
1)  2)
2) 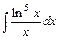 3)
3) 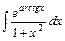
4)  5)
5) 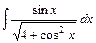
Вариант 9.
1) 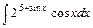 2)
2) 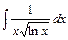 3)
3) 
4) 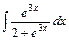 5)
5) 
Вариант 10.
1)  2)
2) 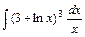 3)
3) 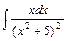
4)  5)
5) 
Вариант 11.
1)  2)
2)  3)
3) 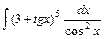
4) 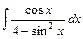 5)
5) 
Вариант 12.
1) 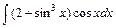 2)
2)  3)
3) 
4)  5)
5) 
Вариант 13.
1) 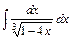 2)
2)  3)
3) 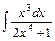
4) 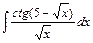 5)
5) 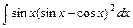
Вариант 14.
1)  2)
2)  3)
3) 
4)  5)
5) 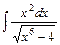
Вариант 15.
1)  2)
2) 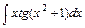 3)
3) 
4) 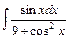 5)
5) 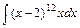
Вариант 16.
1)  2)
2) 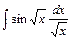 3)
3) 
4)  5)
5) 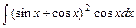
6.3. Найти неопределенный интеграл, используя метод интегрирования по частям.
Вариант 1.
1) 2)
2)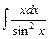 3)
3) 4)
4)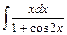
Вариант 2.
1)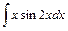 2)
2) 3)
3)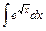 4)
4) 
Вариант 3.
1)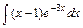 2)
2) 3)
3) 4)
4)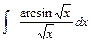
Вариант 4.
1) 2)
2) 3)
3) 4)
4)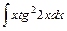
Вариант 5.
1)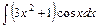 2)
2) 3)
3) 4)
4)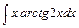
Вариант 6.
1) 2)
2)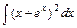 3)
3)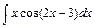 4)
4)
Вариант 7.
1) 2)
2) 3)
3)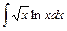 4)
4)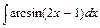
Вариант 8.
1) 2)
2) 3)
3) 4)
4)
Вариант 9.
1) 2)
2) 3)
3) 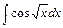 4)
4)
Вариант 10.
1)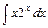 2)
2)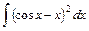 3)
3) 4)
4)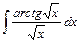
Вариант 11.
1)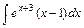 2)
2)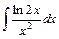 3)
3)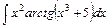 4)
4)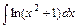
Вариант 12.
1) 2)
2) 3)
3)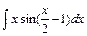 4)
4)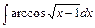
Вариант 13.
1)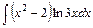 2)
2)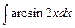 3)
3) 4)
4)
Вариант 14.
1) 2)
2)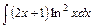 3)
3)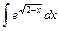 4)
4) 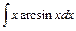
Вариант 15.
1) 2)
2)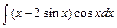 3)
3)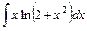 4)
4)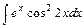
Вариант 16.
1) 2)
2) 3)
3) 4)
4)
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!