Распределение Максвелла

Скорость любой молекулы полностью задаётся трёмя координатами. Поэтому её можно задать как точку в трехмерном пространстве скоростей. Тогда вероятность того, что координаты скорости молекулы будут находиться в определенных интервалах, должна определяться через плотность распределения скорости:

.

При этом должно быть выполнено условие нормировки:

.

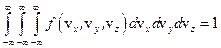Так как каждая из координат скоростей не зависит от других, то плотность распределения должна иметь вид:

,

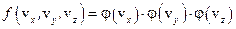где , , .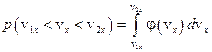

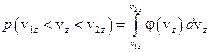Должны быть также выполнены условия нормировки

, , .

Во всех интегралах считается, что проекция скорости принимает любые значения, вплоть до бесконечных. Очевидно, что это не так. Но если подынтегральные функции быстро убывают с ростом значений проекций скорости, то эта добавка будет вносить малую погрешность. Таким образом, к искомым функция предъявляется требование «быстрого убывания на бесконечности». Для поиска вида функции

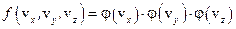
мы применим принцип детального равновесия – в равновесной системе вероятность протекания прямого и обратного процесса одинаковые. Т.е., если формально обратить направление течения времени, то это не повлияет на протекание процессов в системе. Например, если в системе молекула движется в каком-то направлении, то при обращении времени она должны будет двигаться в обратную сторону. Но так как обращение не должно изменять состояния системы, то должна быть такая же молекула, которая до обращения времени уже двигалась в обратном направлении, следовательно, после обращения времени она будет двигаться в прямом направлении. Это означает, что искомая функция может зависеть только от величины скорости молекул, т.е. от . Но в пространстве все направления равноправны. Если повернуть систему координат, то изменятся координаты вектора скорости, но не изменится длина вектора. Потребуем, чтобы функция f не меняла своё значение при повороте системы координат. Таким образом, при должно быть

.

Найдём градиент от искомой функции

.

Рассмотрим вектор, параллельный градиенту (учтем, что ):

.

Т.к. является функцией координат, то .

В трехмерном пространстве скоростей поверхности уровней функций v² и f являются концентрическими сферами с центром в начале координат, поэтому их векторы-градиенты параллельны в каждой точке, следовательно, пропорциональны друг другу:

.

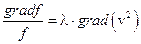В итоге из покоординатных равенств векторов получили систему уравнений:

, , .

После интегрирования этих уравнений, получаем:

, , .

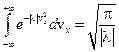Используем условие нормировки: . Этот интеграл - несобственный. Он сходится только в том случае, когда число l - отрицательное: . Интеграл является «табличным»: , поэтому: или .

На каждую степень свободы молекулы приходится энергия . Для идеального газа средняя кинетическая энергия одномерного движения равна: .

С другой стороны

.

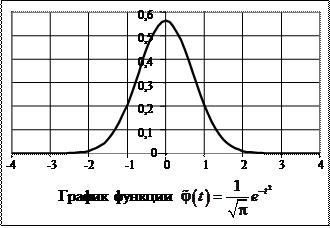
Откуда 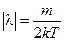и .

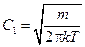Поэтому .

Аналогично , .

В итоге получаем выражение для функции плотности распределения молекул по скоростям:

.

Дата добавления: 2014-01-06