Группировка акционеров по размеру выплаты дивидендов на одну акцию

Первый район	Второй район
АО с размером ди­видендов, руб.	Число АО,в% от их общего количества	АО с размером ди­видендов, руб.	Число АО, в % от их общего количества
10 – 40 40 – 80 80 –120 120 – 160 160 – 200		10 - 60 60 - 120 120 - 200 200 – 300 –	–
Итого		Итого

Приведенные данные не позволяют сравнить распределение акционеров двух районов по размеру дивидендов на одну ак­цию, так как в этих районах имеется различное число групп ак­ционеров, и кроме того, различны величины интервалов. Необ­ходимо ряды интервалов привести к сопоставимому виду. За ос­нову сравнения возьмем структуру распределения акционеров второго района (как наиболее крупную). Следовательно, по пер­вому району нужно произвести вторичную группировку или перегруппировку акционеров, образовав такое же число групп и с теми же интервалами, как во втором районе.

В результате перегруппировки получаем следующие сопоста­вимые данные, характеризующие распределение акционеров двух районов по размеру дивидендов на одну акцию (табл. 3.2.).

Таблица 3.2

Вторичная группировка акционеров по размеру дивидендов на одну акцию (группировка единая)

№ группы	Группы акционеров по размеру дивидендов на акцию, руб.	Удельный вес акционеров группы, %	Расчет
Второй район	Первый район
	10 - 60 60 - 120 120 - 200 200 - 300		–	18 + 0,5 * 12 = 24 0,5 * 12 + 40 = 46 25 + 5 = 30 –
	Итого

Анализ сопоставимых данных вторичной группировки по­зволяет сделать вывод о том, что акционеры второго района имеют более высокие размеры дивидендов (120 руб. и более на одну акцию выплачивают 70%- м акционеров этого района, а в первом районе — только 30%- м акционеров).

3.4. Статистические ряды распределения

После определения группировочного признака и границ групп строится ряд распределения.

Статистический ряд распределения представляет собой упо­рядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характе­ризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.

Ряды распределения, построенные по атрибутивным призна­кам (в порядке возрастания или убывания наблюденных зна­ний), называются атрибутивными. Примером атрибутивных ря­дов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.

Ряды распределения, построенные по количественному признаку, называются вариационными. Например, распределе­ние населения по возрасту, рабочих — по стажу работы, зара­ботной плате и т.д.

Вариационные ряды распределения состоят из двух элемен­тов: вариантов и частот.

Числовые значения количественного признака в вариацион­ном ряду распределения называются вариантами. Они могут быть положительными и отрицательными, абсолютными и от­носительными. Так, при группировке предприятий по результа­там хозяйственной деятельности варианты положительные (при­быль) и отрицательные (убыток) числа.

Частоты — это численности отдельных вариантов или каж­дой группы вариационного ряда, т. е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределе­ния. Сумма всех частот называется объемом совокупности и оп­ределяет число элементов всей совокупности.

Частости — это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%. Замена частот частостями позволяет сопос­тавлять вариационные ряды с разным числом наблюдений.

Вариационные ряды в зависимости от характера вариации под­разделяются на дискретные и интервальные. Дискретные вариаци­онные ряды основаны на дискретных (прерывных) признаках, имеющих только целые значения (например, тарифный разряд ра­бочих, число детей в семье), на дискретных признаках, представ­ленных в виде интервалов; интервальные — на непрерывных при­знаках (имеющих любые значения, в том числе и дробные).

При наличии достаточно большого количества вариантов значений признака первичный ряд является трудно обозримым и непосредственное рассмотрение его не дает представления о распределении единиц по значению признака в совокупности. Поэтому первым шагом в упорядочении первичного ряда явля­ется его ранжирование, т. е. расположение всех вариантов в воз­растающем (или убывающем) порядке.

Например, стаж работы (годы) 22 рабочих бригады характе­ризуется следующими данными:

2, 4, 5, 5, 6, 6, 5, 6, 6, 7, 7, 8, 8, 9, 10, 11, 4, 3, 3, 4, 4, 5

Ранжированный ряд:

2, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 8, 8, 9, 10, 11.

При рассмотрении первичных данных можно видеть, что одинаковые варианты признака у отдельных единиц повторяют­ся (здесь и далее — частота повторений, п — объем изучаемой совокупности).

Способы построения дискретных и интервальных рядов различ­ны. Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака, обозначаемые через х_i, а затем подсчитывается частота повторения каждого варианта . Ряд распределения принято оформлять в виде таблицы, состоящей из двух колонок (или строк), в одной из кото­рых приводятся варианты, а в другой — частоты. Построение дис­кретного вариационного ряда не составляет труда.

Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов «от — до», необходимо установить оптимальное число групп (ин­тервалов), на которое следует разбить все единицы изучаемой со­вокупности. При группировке внутри однокачественной совокуп­ности появляется возможность применения равных интервалов, число которых зависит от вариации признака в совокупности и от количества обследованных единиц.

Проиллюстрируем построение интервального вариационного ряда по данным приведенного выше примера распределения ра­бочих по стажу работы.

Для нашего примера, согласно формулы Стерджесса (3.1), при N = 22 число групп n = 5. Зная число групп, определим ве­личину интервала по формуле (3.2):

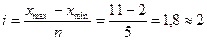. (3.2)

В результате получим следующий ряд распределения рабочих по стажу работы. (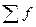= 22):

х... 2 – 4 4– 6 6– 8 8 – 10 10 – 12

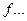3 86 32

Как видно из данного распределения, основная масса рабо­чих имеет стаж работы от 4 до 8 лет.

Ряды распределения удобно изучать с помощью графиче­ского метода.

Контрольные вопросы

1. Что представляют собой первый и второй этапы стати­стического исследования и каковы их значения?

2. Какие виды сводки вы знаете? Дайте их краткую характе­ристику.

3. Что называется статистической группировкой и группировочными признаками?

4. В чем сложность выбора группировочного признака?

5. Какие задачи решает статистика при помощи метода группировок?

6. Дайте характеристику типологических, структурных и аналитических группировок. Какие задачи они решают?

7. В чем выражается взаимосвязь вышеуказанных группировок?

8. Какие группировки называются простыми и сложными и в чем преимущества последних?

9. От чего зависит решение вопроса об определении числа групп и границ интервалов между ними?

10. Какие бывают интервалы группировок и как точно обозначить их границы? Приведите примеры.

11. Что называется вторичной группировкой, в каких случаях приходится прибегать к ней и как можно получить новые группы на основании уже имеющихся?

12. Что представляют собой статистические ряды распределе­ния и по каким признакам они могут быть образованы?

13. Как подразделяются вариационные ряды распределения и на каких признаках они основаны?

14. Какова методика построения дискретных и интервальных ря­дов распределения? Приведите примеры.

Глава 4. Абсолютные и относитель­ные статистические величины

4.1. Абсолютные статистические величины

В итоге сводки статистических данных получают обобщаю­щие статистические показатели, в которых отражаются результа­ты познания количественной стороны массовых общественных явлений. Исходной, первичной формой выражения статистиче­ских показателей, отражающих уровень развития явления, слу­жат абсолютные величины.

Абсолютными в статистике называются суммарные обобщаю­щие показатели, характеризующие размеры (уровни, объемы) об­щественных явлений в конкретных условиях места и времени. Они характеризуют экономическую мощь страны и социальную жизнь населения (ВВП, ВНП, ВНД, реальные располагаемые денежные доходы населения, объемы промышленного и сельскохозяйствен­ного производства, объем выпуска важнейших видов продук­ции). Например, численность населения Российской Федерации на 1 января 1999 г. составила 146,3 млн. человек; в 1998 г. добы­то 303 млн. т нефти (включая газовый конденсат), 591 млрд. м³ ес­тественного газа и т.д.; за 1999 г. ВВП в России составил в теку­щих ценах 4 476 млрд. руб., промышленностью страны за этот пе­риод произведено продукции (работ, услуг) в действующих ценах на сумму 2 995 млрд. руб.

Различают два вида абсолютных величин: индивидуальные и суммарные.

Индивидуальными называют абсолютные величины, характе­ризующие размеры признака у отдельных единиц совокупности (например, размер заработной платы отдельного работника, вклада гражданина в определенном банке и т.д.). Они получа­ются непосредственно в процессе статистического наблюдения и фиксируются в первичных учетных документах.

В отличие от индивидуальных суммарные абсолютные величины характеризуют итоговую величину признака по определенной со­вокупности объектов, охваченных статистическим наблюдением. Они являются суммой количества единиц изучаемой совокупности (численность совокупности) или суммой значений варьирующего признака всех единиц совокупности (объем варьирующего признака).

Абсолютные статистические величины представляют собой именованные числа, т. е. имеют какую-либо единицу измерения.

В зависимости от сущности исследуемого социально-эко­номического явления абсолютные статистические величины выра­жаются в натуральных, стоимостных и трудовых единицах измере­ния. Абсолютные статистические величины могут быть как поло­жительными (доходы), так и отрицательными (убытки, потери).

Натуральные единицы измерения в свою очередь могут быть простыми (тонны, штуки, метры, литры) и сложными, являю­щимися комбинацией нескольких разноименных величин (грузо­оборот железнодорожного транспорта выражается в тонно-кило­метрах, производство электроэнергии — в киловатт-часах, затра­ты труда — в человеко-часах, человеко-днях). В статистике при­меняют и абсолютные показатели, выраженные в условно-натуральных единицах измерения (например, разные виды топ­лива пересчитываются в условное топливо, тракторный парк — в эталонные тракторы).

Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме — рублях. В стоимостных единицах выража­ют валовой выпуск продукции, доходы населения и др.

При использовании стоимостных измерителей принимают во внимание изменение цен с течением времени. Этот недостаток стоимостных измерителей преодолевают применением «неиз­менных» или «сопоставимых» цен одного и того же периода.

В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, тру­доемкость отдельных операций технологического цикла.

4.2. Относительные статистические величины

Наряду с абсолютными статистическими величинами большое значение в статистике имеют относительные величины. В процессе выявления ряда важнейших для социально-экономической жизни вопросов возникает необходимость в изучении структуры явления, соотношения между отдельными его частями, развития во времени.

Относительная величина в статистике — это обобщающий показатель, который представляет собой частное от деления од­ного абсолютного показателя на другой и дает числовую меру соотношения между ними.

Основное условие правильного расчета относительной вели­чины — сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями.

Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.

В зависимости от выбора базы сравнения относительный показатель может быть представлен в различных долях единицы: десятых; сотых (т. е. процентах); тысячных (десятая часть про­цента называется промилле); десятитысячных (сотая часть про­цента называется продецимилле).

Сопоставляемые величины могут быть как одноименными, так и разноименными (в последнем случае их наименования об­разуются от наименований сравниваемых величин, например, руб./чел.; ц/гa; руб./м²).

По своему содержанию относительные величины подразде­ляются на в и д ы: относительные величины динамики, плано­вого задания, структуры, интенсивности, уровня экономиче­ского развития, координации и сравнения.

Относительная величина динамики (i) рассчитывается как от­ношение уровня признака в определенный период или момент времени к уровню этого же признака в предшествующий период или момент времени, т. е. она характеризует изменение уровня какого-либо явления во времени. Относительные величины ди­намики называют темпами роста. Выбор базы сравнения при исчислении относительных показателей динамики определяется целью исследования.

Относительная величина планового задания (i_пл.з) рассчитыва­ется как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в этом периоде.

Относительная величина выполнения плана (i_вып.пл) представляет собой отношение фактически достигнутого в данном пе­риоде уровня к запланированному.

Относительные величины динамики, планового задания и вы­полнения плана связаны соотношением:

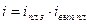
Относительными величинами структуры называются показате­ли, характеризующие долю отдельных частей изучаемой совокуп­ности во всем ее объеме. Они рассчитываются путем деления численности единиц в отдельных частях совокупности на общую численность единиц совокупности (или объем явления). Выра­жаются они простым кратным отношением или в процентах. В качестве примера относительных величин структуры могут слу­жить данные об удельном весе городского населения в общей численности населения России: в 1913 г. — 18%, в 1999 г. — 73%.

Относительными величинами интенсивности называют пока­затели, характеризующие степень распространения или уровень развития того или иного явления в определенной среде. Они вычисляются путем сравнения разноименных величин, находя­щихся в определенной связи между собой. Эти показатели обычно определяются в расчете на 100, 1000 и т.д. единиц изу­чаемой совокупности (на 100 га земли, на 1000 человек населе­ния и т.д.) и являются именованными числами. Примерами могут служить плотность населения, выражающаяся средним числом жителей на одном квадратном километре территории (85,7 чел./км² в России в 1999 г.), обеспеченность населения медицинскими кадрами (численность врачей всех специально­стей 46,7 врача на 10 000 россиян в 1999 г.), возрастные коэф­фициенты рождаемости (число родившихся в среднем за год на 1000 женщин по возрастным группам).

Разновидностью относительных величин интенсивности явля­ются относительные показатели уровня экономического развития, характеризующие уровни ВВП, ВНП, ВНД и других показателей на душу населения и играющие важную роль в оценке развития экономики страны (уровень ВВП Российской Федерации на душу населения в 1999 году составил 30 595 руб. в рыночных ценах).

Относительными величинами координации называют показате­ли, характеризующие соотношение отдельных частей целого между собой. Вычисление этого вида показателей производится путем деления одной части целого на другую часть целого. Та­ким образом, относительные величины координации являются разновидностью относительных величин интенсивности, с той лишь разницей, что они показывают степень распространения, развития разнородных признаков одной и той же совокупности (целого). В зависимости от поставленной задачи тот или иной признак может быть принят за базу. Поэтому для одной и той же совокупности можно исчислить несколько относительных показателей координации.

Относительными величинами сравнения называют показатели, представляющие собой частные от деления одноименных абсо­лютных статистических величин, характеризующих разные объ­екты (предприятия, фирмы, районы, области, страны и т.д.), относящихся к одному и тому же периоду (или моменту) време­ни. Например, соотношение между уровнями себестоимости определенного вида продукции, выпущенной на двух предпри­ятиях, между уровнями производительности труда в разных странах (при одинаковой методике счета).

Рассчитывая относительные величины сравнения, следует об­ращать внимание на сопоставимость сравниваемых показателей с позиции методологии их исчисления, поскольку по целому ряду показателей методы их исчисления в разных странах или в разные периоды времени неодинаковы. Поэтому, прежде чем рассчиты­вать относительные показатели сравнения, приходится решать за­дачу пересчета сравниваемых показателей по единой методологии.

Научная ценность относительных величин высока, но их нельзя рассматривать в отрыве от абсолютных показателей, со­отношения которых они выражают, иначе они не смогут точно характеризовать изучаемые явления.

Пользуясь в анализе относительными величинами, необходимо показать, какие абсолютные величины за ними скрываются. В противном случае можно прийти к неправильным выводам. На­пример, при сравнении двух абсолютных величин 2 тыс. руб. и 5 тыс. руб. получили относительную величину 40%, т. е. 2: 5 * 100. Тот же результат получим, сравнивая 200 тыс. руб. и 500 тыс. руб. Но абсолютное значение одного процента, например второго по­казателя, в том и другом случае будет разным: в первом — оно составит 50, во втором — 5000 руб.

Таким образом, лишь комплексное применение абсолютных и относительных величин выступает как важное средство инфор­мации и анализа самых различных явлений социально-экономической жизни.

Контрольные вопросы

1. Что такое абсолютные статистические величины и каково их значение? Приведите примеры абсолютных величин.

2. Назовите виды статистических показателей. Приведите примеры.

3. В каких единицах измерения выражаются абсолютные ста­тистические величины? Приведите примеры.

4. Всегда ли для анализа изучаемого явления достаточно одних абсолютных показателей?

5. Что называется относительными величинами?

6. Каковы основные условия правильного расчета относитель­ной величины?

7. В какой форме могут быть выражены относительные вели­чины?

8. Какие виды относительных величин вы знаете? Приведите примеры.

Глава 5. Средние величины и показатели вариации

5.1. Понятие о средних величинах

Как правило, многие признаки единиц статистических сово­купностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не оди­накова за один и тот же период времени, различны урожайность сельскохозяйственных культур в хозяйствах района и иены на рынке на одинаковую продукцию и т.д. Поэтому, чтобы опреде­лить значение признака, характерное для всей изучаемой совокуп­ности единиц, прибегают к расчету средних величин.

Средней величиной в статистике называется обобщающий показа­тель, характеризующий типичный уровень явления в конкретных ус­ловиях места и времени, отражающий величину варьирующего при­знака в расчете на единицу качественно однородной совокупности.

В экономической практике используется широкий круг показа­телей, вычисленных в виде средних величин. Например, обоб­щающим показателем доходов рабочих акционерного общества (АО) служит средний доход одного рабочего, определяемый от­ношением фонда заработной платы и выплат социального харак­тера за рассматриваемый период (год, квартал, месяц) к числен­ности рабочих АО. Для лиц с достаточно однородным уровнем доходов, например, работников бюджетной сферы и пенсионеров по старости (исключая имеющих льготы и дополнительные дохо­ды) можно определить типичные доли расходов на покупку предметов питания. Так можно говорить о средней продолжи­тельности рабочего дня, среднем тарифном разряде рабочих, среднем уровне производительности труда и т.д.

Вычисление среднего — один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому мож­но абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обоб­щающих характеристик совокупностей.

Там, где возникает потребность обобщения, расчет таких ха­рактеристик приводит к замене множества различных индивиду­альных значений признака средним показателем, характеризую­щим всю совокупность явлений, что позволяет выявить законо­мерности, присущие массовым общественным явлениям, неза­метные в единичных явлениях.

Средняя отражает характерный, типичный, реальный уро­вень изучаемых явлений, характеризует эти уровни и их изме­нения во времени и в пространстве.

Средняя — это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.

Анализ средних выявляет, например, закономерности изме­нения производительности труда, заработной платы рабочих отдельного предприятия на определенном этапе его экономи­ческого развития, изменения климата в конкретном пункте земного шара на основе многолетних наблюдений средней температуры воздуха и др.

Однако для того, чтобы средний показатель был действи­тельно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из каче­ственно однородных единиц. Это является основным условием на­учно обоснованного использования средних.

Средние, полученные для неоднородных совокупностей, бу­дут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, посколь­ку для его исчисления использована неоднородная совокуп­ность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяю­щим выделить однородные группы, по которым и исчисляют­ся типические групповые средние.

Групповые средние позволяют избежать "огульных" средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д.

Однако нельзя сводить роль средних только к характери­стике типических значений признаков в однородных по данному признаку совокупностях. На практике современная ста­тистика использует так называемые системные средние, обоб­щающие неоднородные явления (характеристики государства, единой народно-хозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу на­селения, среднее потребление продуктов питания на душу на­селения, производительность общественного труда).

В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности от­дельных хозяйствующих субъектов, и ростки нового, прогрессив­ного. Так, например, распределение населения по доходу позволя­ет выявлять формирование новых социальных групп. Поэтому на­ряду со средними статистическими данными необходимо учиты­вать особенности отдельных единиц совокупности.

Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, так как в этом случае согласно закону больших чисел взаимопогашаются случайные, индивидуальные различия между единицами, и они не оказы­вают существенного влияния на среднее значение, что способ­ствует проявлению основного, существенного, присущего всей массе. Если основываться на средней из небольшой группы данных, то можно сделать неправильные выводы, поскольку та­кой средний показатель будет отражать значительное влияние индивидуальных особенностей, т.е. случайных моментов, не ха­рактерных для изучаемой совокупности в целом.

Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных осо­бенностей нужна система средних показателей. Поэтому в практи­ке отечественной статистики для изучения социально-экономичес­ких явлений, как правило, исчисляется система средних показате­лей. Так, например, показатели средней заработной платы оцени­ваются совместно с показателями средней выработки, фондово­оруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.

Средняя должна вычисляться с учетом экономического содер­жания исследуемого показателя. Поэтому для конкретного показа­теля, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе науч­ного способа расчета.

5.2. Виды средних и способы их вычисления

Выбор вида средней определяется экономическим содержа­нием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних вели­чин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.

Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (при различных значениях m):

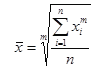, (5.1)

где 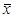– среднее значение исследуемого явления;

т – показатель степени средней;

x – текущее значение (вариант) осредняемого признака;

п – число признаков.

В зависимости от значения показателя степени т различают следующие виды степенных средних:

При т = -1 – средняя гармоническая;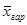

при т = 0 – средняя геометрическая ;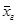

при т = 1 – средняя арифметическая ;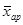

при т = 2 – средняя квадратическая ;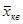

при т = 3 – средняя кубическая .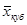

При использовании одних и тех же исходных данных, чем больше т в формуле (5.1), тем больше значение средней величины:

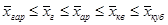(5.2)

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в стати­стике правилом мажорантности средних.

Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид сред­ней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материаль­ным содержанием изучаемого явления, а также принципами суммирования и взвешивания.

Помимо степенных средних в статистической практике ис­пользуются средние структурные, в качестве кото­рых рассматриваются мода и медиана.

Остановимся подробнее на степенных средних.

5.2.1. Средняя арифметическая

Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общест­венных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область при­менения средней арифметической и объясняется ее распро­страненность как обобщающего показателя. Так, например, общий фонд заработной платы – это сумма заработных плат всех работников, валовой сбор урожая – сумма произведенной продукции со всей посевной площади.

Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.

Средняя арифметическая применяется в фор­ме простой средней и взвешенной средней. Исходной, опреде­ляющей формой, служит простая средняя.

Ø Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеют­ся несгруппированные индивидуальные значения признака):

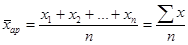, (5.3)

где x₁, x₂, …, x_n – индивидуальные значения варьирующего признака (варианты);

п ­ – число единиц совокупности.

Например, требуется найти среднюю выработку одного ра­бочего (слесаря), если известно, сколько деталей изготовил каж­дый из 15 рабочих, т.е. дан ряд индивидуальных значений при­знака, шт.:

21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.

Средняя арифметическая простая рассчитывается по формуле (5.3), шт.:

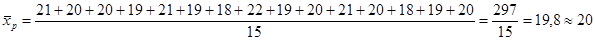
Средняя из вариантов, которые повторяются различное чис­ло раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

Ø Средняя арифметическая взвешенная – средняя сгруппи­рованных величин x₁, x₂, …, x_n – вычисляется по формуле:

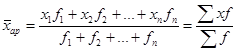, (5.4)

где 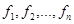– веса (частоты повторения одинаковых признаков);

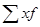– сумма произведений величины признаков на их частоты;

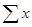– общая численность единиц совокупности.

Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим их в табл. 5.1.

Таблица 5.1

Дата добавления: 2014-01-06