
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинематика вращательного движения
|
|
|
|
Поступательное движение твердого тела
При поступательном движении твердого тела все его точки тела имеют одинаковые (совпадающие при наложении) траектории, одинаковые по численному значению и направлению скорости и ускорения. Поэтому рассмотренные выше кинематические характеристики материальной точки целиком и полностью применимы к поступательному движению твердого тела.
При описании вращательного движения удобно пользоваться полярными координатами  и
и 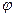 , где
, где  - радиус (расстояние от центра вращения до точки),
- радиус (расстояние от центра вращения до точки), 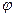 - полярный угол (угол поворота).
- полярный угол (угол поворота).
Угловое перемещение – аксиальный скользящий вектор, модуль которого равен углу поворота, направление определяется правилом правого винта, а модуль равен углу поворота. При малых углах поворота
 (1.1.18)
Угловая скорость: (1.1.18)
Угловая скорость:  , (1.1.19) , (1.1.19)
|  Рис.1.5 Рис.1.5
|
Угловое ускорение: 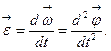 (1.1.20)
(1.1.20)
Единицы углового перемещения, угловой скорости и углового ускорения -  .
.
Векторы  и
и  лежат на оси вращения. Направление вектора
лежат на оси вращения. Направление вектора  совпадает с направлением вектора
совпадает с направлением вектора  . Вектор
. Вектор  направлен в сторону вектора
направлен в сторону вектора  при ускоренном движении и противоположен ему при замедленном (рис.1.5).
при ускоренном движении и противоположен ему при замедленном (рис.1.5).
В случае равнопеременного вращения тела ( ) из (1.1.20)
) из (1.1.20)  получаем закон скорости:
получаем закон скорости:  (1.1.21)
(1.1.21)
Подставив (1.1.21) в (1.1.19), получим: 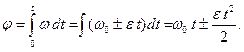 (1.1.22)
(1.1.22)
Установим связь между линейными и угловыми кинематическими характеристиками точки. Если за время  точка
точка 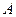 описала дугу
описала дугу 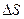 (рис.1.6), то модуль ее линейной скорости (с учетом (1.1.3) и (1.1.18)) равен:
(рис.1.6), то модуль ее линейной скорости (с учетом (1.1.3) и (1.1.18)) равен:  (1.1.23)
(1.1.23)
 Рис.1.6 Рис.1.6
| В векторном виде последняя формула имеет вид:
 . (1.1.24)
Тангенциальное ускорение . (1.1.24)
Тангенциальное ускорение  связано с угловым ускорением связано с угловым ускорением 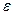 : :
 или или 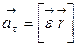 . (1.1.25)
Нормальное ускорение . (1.1.25)
Нормальное ускорение
|
 или
или  . (1.1.26)
. (1.1.26)
В табл. 1.2 приведены кинематические характеристики тела при поступательном и вращательном движениях.
Таблица 1.2
| Поступательное Движение | Вращательное Движение | Связь между характеристиками | ||
| Радиус-вектор | 
| Угол поворота | 
| |
| Вектор перемещения | 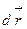
| Вектор углового перемещения | 
| |
| Длина пути | 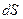
| Длина пути | 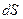
| 
|
| Скорость | 
| Угловая скорость | 
| 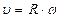
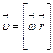
|
| Ускорение |  
| Угловое ускорение | 
| |
| Тангенц. ускорение | 
| 

| ||
| Нормальное ускорение | 
| 

|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 426; Нарушение авторских прав?; Мы поможем в написании вашей работы!