Абсолютно упругий удар шаров

Рассмотрим абсолютно упругий удар шаров, при котором происходит упругая деформация шаров, не возникает тепла и пластической деформации (рис.8.3). Даны массы шаров и их скорости до удара 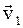, . В результате такого взаимодействия вся кинетическая энергия до удара превращается в кинетическую энергию системы (шаров) после удара. В результате после удара шары будут двигаться с некоторыми скоростями u₁ и u₂.

Пусть . Шары взаимодействуют только между собой, т.е. система замкнута, между телами действуют только консервативные силы.

В такой ситуации должны выполняться законы сохранения импульса и механической энергии. Запишем эти законы применительно к данному случаю, причем закон сохранения импульса представим в алгебраической форме:

. (8.46)

Перепишем эти формулы следующим образом:

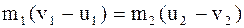; (8.47)

. (8.48)

Разделим (8.48) на (8.47) почленно:

. (8.49)

Теперь имеем систему линейных уравнений (8.47) и (8.49). Для нахождения скоростей шаров после взаимодействия 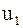, выразим из (8.49) и подставим в (8.47):

, .

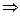
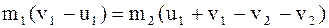Откуда

. (8.50)

В системе уравнений (8.46) ничего не изменится, если заменить индекс 1 на индекс 2, поэтому для получения формулы, выражающей , достаточно в формуле (8.50) заменить индекс 1 на индекс 2:

. (8.51)

В общем случае

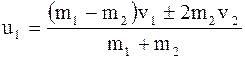; (8.52)

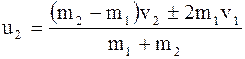. (8.53)

Знак (+) соответствует случаю, когда первый шар нагоняет второй, а знак (-) - когда шары движутся навстречу друг другу.

Из уравнения (8.53) видно, что:

1) если m₁ = m₂ = m, то u₁ = v₂, а u₂ = v₁, т.е. в этом случае шары обмениваются скоростями;

2) при ударе шара о стенку (m₂>>m₁):

а) u₂ = v₂ - скорость стенки остается неизменной;

б) u₁ = 2v₂ – v₁ - при этом, если стенка неподвижна (v₂ = 0), скорость шара после удара, оставаясь неизменной по величине, изменяет свое направление на противоположное. При v₂ = 0 u₁ возрастает до 2v₂ при движении стенки навстречу шару и убывает до 2v₂, если стенка удаляется от него.

Дата добавления: 2014-01-06