Математические модели биполярных транзисторов

Моделированием материального объекта (структуры, процесса, системы) называется представление этого объекта символическим описанием или другим объектом, которые замещают моделируемый объект в отношении исследуемых свойств на некоторой ступени познавательного процесса.

Различают два основных типа моделей транзистора:

1. Математическая модель, которая даёт символическое математическое описание процессов в транзисторе. Это абстракция, позволяющая лишь мысленно анализировать процессы, происходящие в транзисторе. Однако эта модель отражает с требуемой точностью реальные процессы в приборе.

2. Физическая (аналоговая) модель, в которой физические процессы в транзисторе заменяют другими, более удобными для исследования.

Это реальное физическое устройство для изучения процессов в моделируемом объекте.

Возможности математических моделей по исследованию процессов в транзисторах значительно превышают возможности физических моделей.

С помощью математической модели можно без больших материальных затрат провести анализ многих вариантов построения транзисторов и транзисторных цепей.

Поэтому основным типом модели транзистора является математическая или в дальнейшем просто «модель».

Все «модели» транзистора,взависимости от исследуемого режима работы транзистора, могут быть разделены на два класса:

1. Статические модели, описывающие свойства транзистора на постоянном токе (модели в режиме большого сигнала);

2. Динамические модели, описывающие свойства транзистора на переменном электрическом сигнале при малых амплитудах сигналов (модели в режимах малых сигналов).

Критерием малого сигнала при построении моделей принято считать амплитуды переменных напряжений, действующих в цепи база-эмиттер, достаточно меньших по сравнению со значением температурного потенциала φ_Т в уравнении Шокли (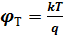, при t = +27˚С φ_Т = 25мВ).

Модель транзистора для большого сигнала (модель Эберса-Молла).

В качестве такой модели наибольшее распространение получила модель Эберса-Молла, которая основывается на уравнении диода (уравнении Шокли). Эта модель при достаточно высокой точности является наименее сложной (содержит минимальное количество элементов с легко измеряемыми параметрами).

Общая эквивалентная схема транзистора, используемая при получении математической модели Эберса-Молла, показана на писунке.

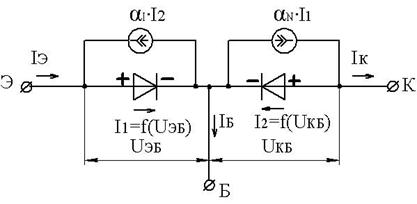
Каждый переход транзистора p-n-p типа представлен в виде диода, а их взаимодействие отражено генераторами токов, где:

α_I – инверсный коэффициент передачи тока (из коллектора в эмиттер);

α_N – нормальный коэффициент передачи тока (из эмиттера в коллектор)

α_NI₁ – генератор коллекторного тока при нормальном включении;

α_II₂ – генератор эмиттерного тока при инверсном включении.

Таким образом, токи эмиттера и коллектора в общем случае содержат две составляющие: инжектируемую (α_I или α_N) и экстрактируемую (α_NI₁или

α_II₂), поэтому:

; (1)

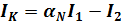(2)

Если в общей эквивалентной схеме поочередно прикладывать напряжение к каждому p-n переходу, а выводы других, соответственно, поочередно замыкать между собой накоротко, то токи I₁и I₂, протекающие через p-n переходы к которым приложено напряжение (в соответствии с уревнением Шокли) примут вид:

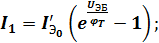(3)

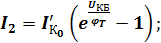(4)

где 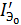- тепловой ток эмиттерного p-n перехода при замкнутых базе и коллекторе;

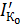- тепловой ток коллекторного p-n перехода при замкнутых базе и эмиттере.

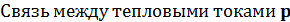−n переходов 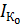, , 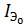включенных раздельно и тепловыми токами получим из (1) и (2).

Пусть 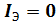, тогда .

При .

Подставив эти выражения в (1) и (2) для тока коллектора получим:

,

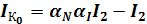учитывая, что имеем:

,

;

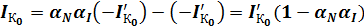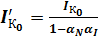Аналогично: .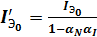

Токи коллектора и эмиттера с учетом (3) и (4) будут:

;

;

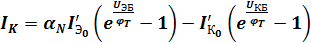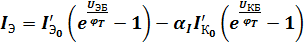На основании закона Кирхгофа ток базы будет: ;

.

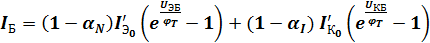В самом общем случае в транзисторах справедливо равенство:

,

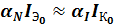тогда при ,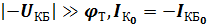

поэтому

.

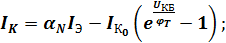
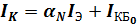Последние уравнения описывают выходные ВАХ транзистора.

Из уравнения для определения I_Э, решенное относительно U_ЭБ, получим выражение для идеализированных входных характеристик транзистора:

.

Учитывая, что обычно 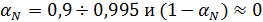, последнее уравнение может быть упрощено:

.

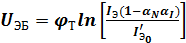Модели Эберса-Молла, несмотря на их приближенность, очень полезны для анализа статических режимов при больших изменениях сигналов, так как они нелинейные.

Дата добавления: 2014-01-06