Получение однофазной синусоидальной э.д.с

Поместим рамку, состоящую из одного витка, в однородное поле постоянных магнитов (рис. 2.1). Рамка вращается с постоянной угловой скоростью ω =const. В соответствии с законом электромагнитной индукции в ней будет наводиться э.д.с:

,

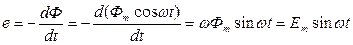где:

Ф_m – амплитудное (максимальное) значение магнитного потока;

α = ωt – угол между направлением поля и нормалью к плоскости рамки;

Е_m = ωФ _m– амплитудное (максимальное) значение э.д.с.

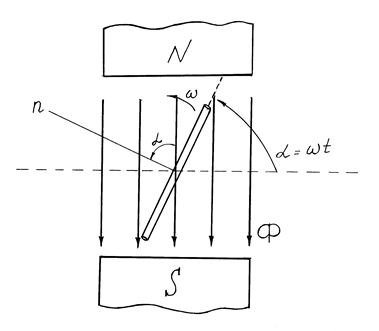
Рис. 2.1. Рамка в однородном поле

Синусоидальную функцию времени можно выразить:

1) графиком (рис. 2.2);

2) уравнением e = E _m sin ωt;

3) вращающимся вектором, называемым радиус-вектором (рис. 2.3).

Период Т (рис. 2.2) – интервал времени, в течение которого функция проходит полный цикл своего изменения.

Рис. 2.2. График изменения синусоидальной э.д.с. во времени

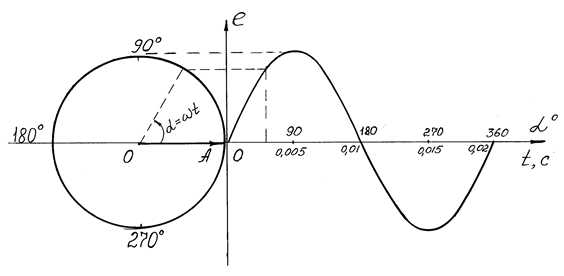
Рис. 2.3. Получение синусоиды путем вращения вектора

Частота – величина, обратная периоду, численно равна числу периодов в одну секунду. Единица измерения – герц (Гц =1/с).

Мгновенные значения – значения изменяющихся во времени э.д.с, тока, напряжения, мощности в любой момент времени. На протяжении одного периода можно взять бесчисленное множество мгновенных значений. Мгновенные значения обозначаются строчными буквами: е,i,u, р.

Амплитудное значение – наибольшее мгновенное значение синусоидальной э.д.с. тока, напряжения, мощности, обозначается прописной буквой с индексом т (max): E_m, I_m, U_m, P_m.

Рассмотрим получение синусоиды путем вращения вектора (рис. 2.3). Допустим, что вектор ОА соответствует максимальному значению Е_т синусоидальной функции e = E _m sin ωt и вращается против часовой стрелки с угловой скоростью ω, а угол α = ωt непрерывно изменяется. Проекция вектора ОА на вертикальную ось равна: e = OA·sin α = OA·sin ωt = E _m sin ωt.

Аргумент синуса, т.е. величина ωt (может быть ωt + ψ) называется фазой, где ψ – начальная фаза.

Величина [1/c] получила название угловой частоты. Для промышленной частоты f = 50 Гц, ω = 2·3,14·50=314 (1/с).

Если две синусоидально изменяющиеся величины проходят в одно и то же время через нулевые и максимальные значения, то эти две величины совпадают по фазе (рис. 2.4).

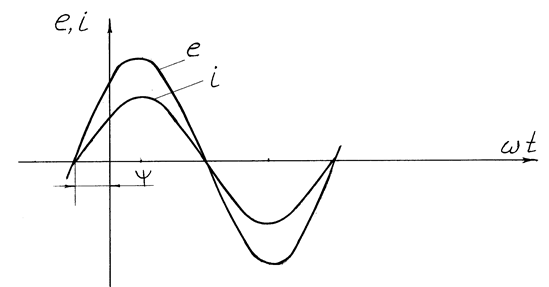
Рис. 2.4. Синусоидальные величины, совпадающие по фазе

Если e = E _m sin (ωt – ψ ₁), а I = I _m sin (ωt – ψ ₂ ), то эти две величины не будут совпадать по фазе (рис. 2.5). Угол ψ ₁ – ψ ₂ = φ называется углом сдвига по фазе.

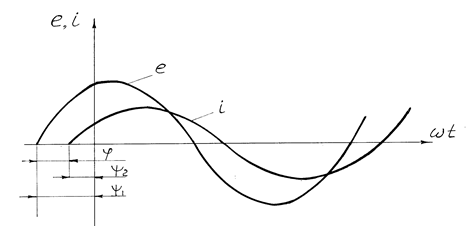
Рис. 2.5. Синусоидальные величины, несовпадающие по фазе

Дата добавления: 2014-01-06