Приклади поверхонь обертання

Циліндрична поверхня обертання (поверхня прямого кругового циліндра)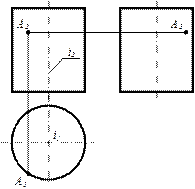

	Конус обертання
Поверхня кулі (сфера). Поверхня утворюеться обертанням кола навколо свого діаметра.

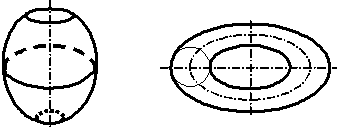
Торова поверхня.

Утворюється обертанням кола або її дуги навколо осі, що не проходить через центр кола.

Закритий тор Відкритий тор.

8.2. Перетин поверхні обертання площиною. Фігури перерізу.

Сфера.

Розріз сфери в усіх випадках являє собою коло, що у залежності від розташування січної площини може або проектуватися без спотворення, або у вигляді еліпса (січна площина нахилена до площини проекцій під кутом, не рівним 90º), або у вигляді прямої лінії (січна площина перпендикулярна площини проекцій).

Циліндрична поверхня.

Переріз циліндра обертання в залежності від положення січної площини може являти собою:

1) дві прямі (утворюючі) – якщо січна площина рівнобіжна осі циліндра (s ^1); 2) коло – якщо січна площина перпендикулярна осі циліндра (s ^2); 3) еліпс – якщо січна площина нахилена до осі циліндра(s ^3).

Конічна поверхня.

Перерізи конічної поверхні обертання площиною називаються конічними перерізами і являють собою повний набір кривих 2-го порядку. У залежності від положення січної площини стосовно елементів поверхні (осі, утворюючої), фігури перерізів можуть являти собою:

1) дві прямі (утворюючі) – якщо січна площина проходить через вершину конуса (s ¹);

2) коло – якщо січна площина перпендикулярна осі конуса (s ²);

3) Парабола – якщо січна площина паралельна одній з утворюючих конуса (s ³);

4) еліпс – якщо січна площина перетинає всі утворюючі конуса (кут нахилу січної площини (s ⁴) до осі конуса більше, ніж кут нахилу утворюючої);

5) гіпербола – якщо січна площина рівнобіжна двом утворюючім конуса (кут нахилу січної площини (s ⁵) до осі конуса менше, ніж кут нахилу утворюючої або дорівнює нулю).

8.3. Побудова проекцій і істинного вигляду переріза поверхонь обертання площиною.

Побудувати проекції й істинний вид розрізу заданого геометричного тіла площиною σ _2.

Задане геометричне тіло складається з двох поверхонь: - півсфери, - усіченого конуса У перетині сфери - завжди коло (у даному випадку, дуга). Форма розрізу конічної поверхні залежить від розташування січної площини (у даному випадку це парабола). Побудову починають із визначення характерних (опорних) точок: т. 1, 2-3, 4-5, 6-7. Проміжні точки: 8-9. Істинний вигляд перетину визначаємо методом заміни площин проекцій.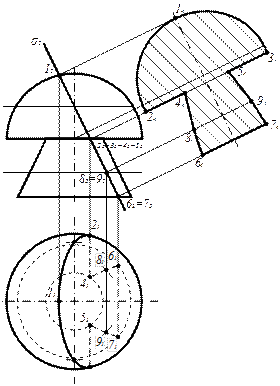

8.4. Перетинання прямої лінії з поверхнею.

Для побудови точок перетинання прямої із поверхнею застосовується той же алгоритм, що і для розв'язання аналогічної задачі з багатогранником. Розходження полягає лише у формі фігури розрізу.

Для ілюстрації обмежимося наочним малюнком.

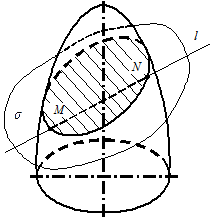8.5. Геометричні тіла з вирізами.

У даній темі розглянемо побудову проекцій геометричних тіл із вирізами, утвореними плоскими поверхнями. У цьому випадку задача зводиться до побудови плоских розрізів заданого геометричного тіла, які утворяться при перетинанні його з кожній із площин, що утворюють виріз.

Раніш, чим приступити безпосередньо до побудови, необхідно проаналізувавши задану фігуру, визначити, які форми розрізів повинні утворитися. Потім будують послідовно лінії перетинів, починаючи з визначення опорних точок. Закінчується розв'язання задачі визначенням видимості.

Дата добавления: 2014-01-06