Функция возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2

Для умножения матриц используется стандартная функция МУМНОЖ.

Умножение матриц в Microsoft Excel.

МУМНОЖ (массив1; массив2)

Массив1, массив2 — перемножаемые массивы(матрицы).

Замечание. Количество столбцов аргумента массив1 должно быть таким же, как количество сток аргумента массив2, и оба массива должны содержать только числа.

Решение примера 1.1 в Microsoft Excel:

1) Запускаем Microsoft Excel.

2) Вводим матрицы в виде массивов чисел. Матрица А записывается в диапазоне ячеек А2:С3. Матрица В записывается в диапазоне ячеек А5:В7.

3) Поскольку матрица А содержит 3 столбца а матрица В содержит 3 строки, то произведение АВ существует. Результатом умножения матрицы А на матрицу В будет матрица С, размерности 2х2, т.е. . Поэтому подготовим диапазон ячеек куда будет выведен массив чисел матрицы С, для этого выделим ячейки В9:С10.

4) В меню Вставка>Функция выбираем функцию МУМНОЖ (она находится в математических функциях). Вводим в поле массив1 диапазон ячеек А2:С3 а в поле массив2 диапазон А5:В7. Нажимаем ОК, затем для корректного вывода массива чисел нажимаем клавишу F2, а затем сочетание клавиши CTRL+SHIFT+ENTER.

5) В результате выполненных операций диапазон ячеек В9:С10 будут записаны элементы матрицы .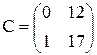

Аналогично найдём произведение ВА.

6) Поскольку матрица В содержит 2 столбца а матрица А содержит 2 строки, то произведение АВ существует. Результатом умножения матрицы В на матрицу А будет матрица D, размерности 3х3, т.е. . Поэтому подготовим диапазон ячеек куда будет выведен массив чисел матрицы D, для этого выделим ячейки B12:D14.

7) В меню Вставка>Функция выбираем функцию МУМНОЖ. Вводим в поле массив1 диапазон ячеек А5:В7 а в поле массив2 диапазон А2:С3. Нажимаем ОК, затем для корректного вывода массива чисел нажимаем клавишу F2, а затем сочетание клавиши CTRL+SHIFT+ENTER.

8) В результате выполненных операций диапазон ячеек B12:D14 будут записаны элементы матрицы .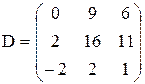

2. НАХОЖДЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ.

Определителем матрицы первого порядка , или определителем первого порядка, называется элемент :

.

Определителем квадратной матрицы второго порядка , или определителем второго порядка, называется число, которое вычисляется по формуле:

.

Пусть дана квадратная матрица третьего порядка:

.

Определителем матрицы третьего порядка А, или определителем третьего порядка, называется число, которое вычисляется по формуле:

.

Определители квадратных матриц более высоких порядков определяются по теореме Лапласа.

Пример 1.2. Даны матрицы , , .

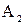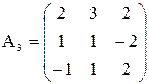
Найти -?

Решение:

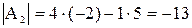
Дата добавления: 2014-01-06