Базисное решение

Метод Гаусса.

Метод Крамера.

Метод обратной матрицы.

Система 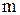линейных алгебраических уравнений с 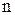переменными имеет вид:

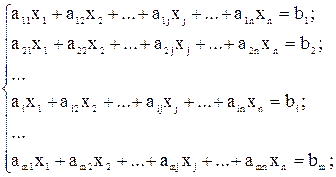(2.1)

где 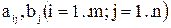- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений. Решением системы называется такая совокупность 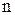членов 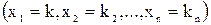, при подстановке которых каждое уравнение системы обращается в верное равенство.

1. МЕТОД ОБРАТНОЙ МАТРИЦЫ.

Запишем систему (2.1) в матричной форме. Обозначим:

; ; ,

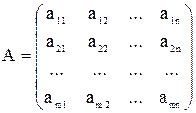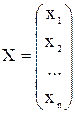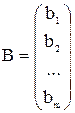где А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных; В – матрица-стоблец свободных членов. Таким образом систему (2.1) можно записать в виде:

АХ=В (2.2)

Для получения решения системы при (2.1) при 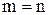в общем виде предположим, что квадратная матрица системы 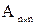невырожденная, т.е. ее определитель 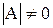. В этом случае существует обратная матрица .

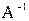Умножая слева обе части матричного равенства (2.2) на матрицу 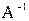, получим 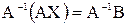. Так как 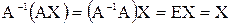, то решение системы методом обратной матрицы будет матрица-столбец:

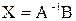
Таким образом, для решения СЛАУ методом обратной матрицы можно составить следующий алгоритм:

1) Для заданной СЛАУ записать отдельно матрицы А (матрицу системы) и матрицу В (матрица-столбец свободных членов);

2) Найти определитель матрицы А, если 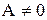, тогда существует обратная матрица 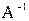, иначе решения не существует;

3) Найти обратную матрицу ;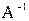

4) Используя формулу 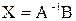найти матрицу столбец Х, путём умножения обратной матрицы 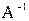на матрицу-столбец свободных членов В.

5) Проверить найденный результат по формуле 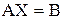, т.е. при умножении матрицы системы А на найденную матрицу-столбец Х мы должны получить матрицу-столбец свободных членов В (пункт 5 не обязателен).

Пример 2.1. Решить систему линейных алгебраических уравнений методом обратной матрицы.

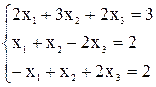
Решение:

Для решения воспользуемся описанным выше алгоритмом.

1) Обозначим

; ; .

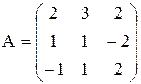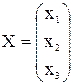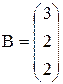2) Найдем определитель 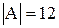(см. пример 1.2. ПРАКТИЧЕСКАЯ РАБОТА 1), так как 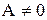, то матрица - невырожденная, и существует обратная матрица .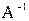

3) Матрицу 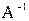находим по алгоритму, приведённому в ПРАКТИЧЕСКОЙ РАБОТЕ 1 (см. пример 1.3.). Получим:

4) Теперь, по формуле 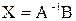(умножение матриц описано в примере 1.1. ПРАКТИЧЕСКАЯ РАБОТА 1) найдем искомую матрицу-столбец переменных:

Т.е. решение системы , , .

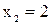Решение примера 2.1. в Microsoft Excel:

1) Запускаем Microsoft Excel. В ячейки А2:С4 вводим матрицу А, в ячейки 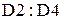вводим матрицу-столбец В.

2) Найдем определитель матрицы А (см. решение примера 2.1. в Microsoft Excel ПРАКТИЧЕСКОЕ ЗАДАНИЕ 1). В ячейке А7 при помощи функции МОПРЕД находим определитель матрицы А. Матрица А невырожденная, так как найденный определитель равен 12, поэтому обратная матрица существует.

3) Найдем обратную матрицу 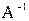(см. решение примера 1.3. в Microsoft Excel ПРАКТИЧЕСКОЕ ЗАДАНИЕ 1). Выделим диапазон ячеек А10:С12, используем функцию МОБР. В результате получим обратную матрицу, содержащую элементы:

.

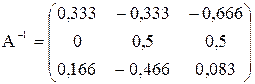4) Найдем искомую матрицу-столбец переменных Х по формуле 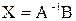. Для этого необходимо умножить обратную матрицу 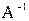на матрицу В (см. решение примера 1.1. в Microsoft Excel ПРАКТИЧЕСКОЕ ЗАДАНИЕ 1). Выделим ячейки А15:А17. Для этого используем функцию МУМОЖ. В результате получим матрицу-стоблец Х, содержащую элементы:

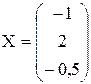
5) Сделаем проверку. Умножим исходную матрицу А на найденную матрицу Х. Выделим диапазон ячеек А20:А22, используем функцию МУМНОЖ. В результате получим матрицу столбец

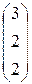
Найденные элементы совпадают с матрицей-столбцом свободных членов В. Следовательно решение найдено верно.

2. МЕТОД КРАМЕРА.

Пусть 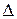- определитель матрицы системы А, а 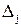- определитель матрицы, получаемой из матрицы А заменой 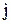-ого столбца столбцом свободных членов. Тогда, если 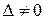, то система имеет единственное решение, определяемое по формулам:

.

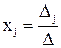
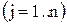Таким образом, для решения СЛАУ методом Крамера можно составить следующий алгоритм:

1) Для заданной СЛАУ записать и найти определитель системы 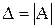, если 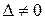, то система имеет единственное решение;

2) Записать определители 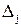матриц, которые получаются из матрицы А заменой 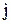-ого столбца столбцом свободных членов. Найти определители ;

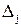3) По формуле 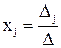найти решение системы.

Пример 2.2. Решить систему линейных алгебраических уравнений методом Крамера.

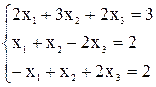
Решение:

Для решения воспользуемся описанным выше алгоритмом:

1) Определитель системы 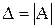для заданной системы имеет вид:

т.е. 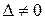, следовательно, система имеет решение.

2) Найдем определители ,,: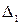

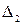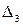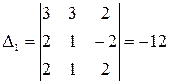
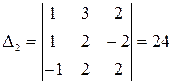
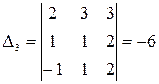
3) Теперь по формуле 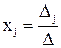найдем решение системы:

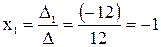
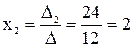
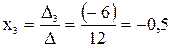
Решение примера 2.2. в Microsoft Excel:

1) Запускаем Microsoft Excel, если он уже запущен, то переходим на новый лист. Вводим в диапазон ячеек А2:С4 матрицу системы А, выделяем ячейку 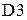и находим определитель 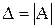при помощи функции МОПРЕД (см. решение примера 2.1. в Microsoft Excel ПРАКТИЧЕСКОЕ ЗАДАНИЕ 1). В результате получаем 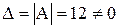, следовательно решение существует.

2) В диапазоны ячеек А7:С9, А12:С14, А17:С19 вводим соответственно матрицы, которые получаются заменой первого, второго, и третьего столбца столбцом свободных членов. Находим определители 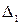,,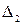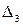этих матриц в ячейках 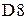, , 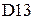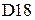соответственно, при помощи функции МОПРЕД, получаем соответственно -12, 24, -6.

3) Теперь по формуле 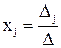в ячейках В22, В23, В24 находим соответственно 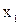, , 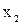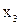получаем -1, 2, -0,5 соответственно.

2. МЕТОД ГАУССА.

Метод Гаусса – метод последовательного исключения – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Предположим что в системе (2.1) коэффициент при переменной 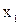в первом уравнении 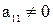(если это не так, то перестановкой уравнений местами добьемся того, что ).

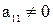Шаг 1. Умножим первое уравнение на подходящие числа (а именно на 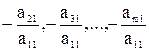) и прибавляя полученные уравнения соответственно ко второму, третьему, …, 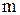-му уравнению системы (2.1), исключим первую переменную 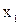из всех последующих уравнений, начиная со второго. Получим:

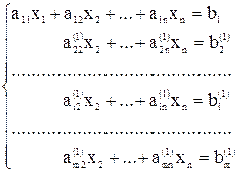
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.

Шаг 2. Предположим, что 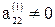(если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьемся того, чтобы ).

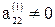Умножая второе уравнение на подходящие числа (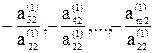) и прибавляя полученные уравнения соответственно к третьему, четвертому,…, 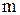-ому уравнению системы, исключим переменную 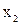из всех последующих уравнений, начиная с третьего.

Продолжая процесс последовательно исключения переменных 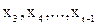, после 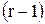-го шага получим систему:

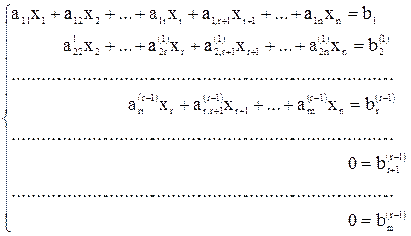(2.3)

Число нуль в последних 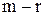уравнениях означает, что их левые части имеют вид 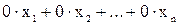. Если хотя бы одно из чисел не равно нулю, то соответствующее равенство противоречиво, и система (2.1) несовместна (т.е. решений нет).

Таким образом, для любой совместно системы числа в последней системе равны нулю. В этом случае последние 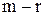уравнений в этой системе являются тождествами и их можно не принимать во внимание при решении системы (2.1). Очевидно, что после отбрасывания «лишних» уравнений возможны два случая: а) число уравнений системы (2.3) равно числу переменных, т.е. 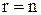(в этом случае система (2.3) имеет треугольный вид); б) 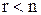(в этом случае система (2.3) имеет ступенчатый вид).

Переход системы (2.1) к равносильной ей системе (2.3) называется прямым ходом метода Гаусса, а нахождение переменных системы – обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов.

Пример 2.3. Решить систему линейных алгебраических уравнений методом Гаусса.

Решение.

Расширенная матрица системы имеет вид:

.

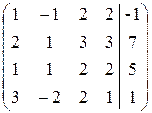Шаг 1. Так как 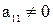, то умножая первую строку на 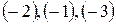(так как 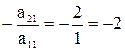, , 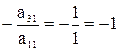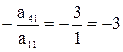) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную 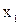из всех строк, начиная со второй.

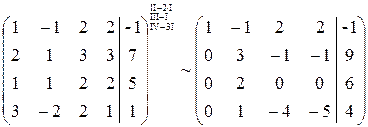
Шаг 2. Так как 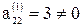, то умножая вторую строку на 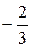, 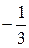(так как 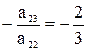, 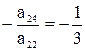) и прибавляя полученные строки к третей и четвертой, исключим переменную 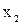из всех строк, начиная с третьей:

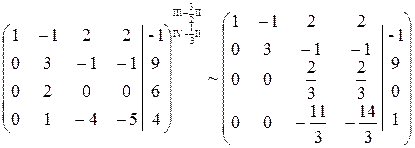
Шаг 3. Учитывая, что 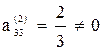, умножаем третью строку на 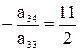и прибавляя полученную строку к четвертой, исключим из нее переменную :

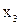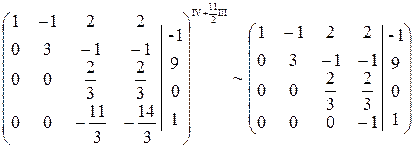
Получим эквивалентную систему уравнений:

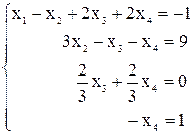
откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения , из третьего , из второго и из первого уравнения 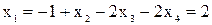. Таким образом, решение системы .

Дата добавления: 2014-01-06