
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратичная форма. Исследование на знакоопределенность квадратичной формы
|
|
|
|
Линейный оператор. Собственные значения и собственные векторы линейных операторов.
Проверка на базис.
Сложение, вычитание векторов, угол между векторами, скалярное произведение векторов.
ТЕМА 3: ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА.
1. СЛОЖЕНИЕ, ВЫЧИТАНИЕ ВЕКТОРОВ, УГОЛ МЕЖДУ ВЕКТОРАМИ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Суммой двух векторов  и
и  называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец с концом вектора
, а конец с концом вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (рис 1) (правило треугольников).
(рис 1) (правило треугольников).
Очевидно, что вектор  в этом случае представляет диагональ параллелограмма, построенного на векторах
в этом случае представляет диагональ параллелограмма, построенного на векторах  и
и  (рис 1) (правило параллелограмма).
(рис 1) (правило параллелограмма).

Рис. 1.
Разностью двух векторов  и
и  называется сумма вектора
называется сумма вектора  и вектора
и вектора  , противоположного
, противоположного  . Легко убедится в том, что на параллелограмме, построенном на векторах
. Легко убедится в том, что на параллелограмме, построенном на векторах  и
и  это будет другая диагональ (рис 2).
это будет другая диагональ (рис 2).
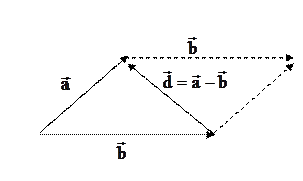
Рис. 2.
Координатами вектора  называются координаты его конечной точки.
называются координаты его конечной точки.


Если 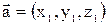 и
и 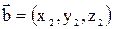 , то суммой и разностью являются соответственно векторы:
, то суммой и разностью являются соответственно векторы:

А произведение вектора 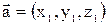 на число
на число  есть вектор
есть вектор  .
.
Длина вектора равна корню квадратному его из суммы квадратов его координат:

Скалярным произведением 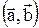 двух векторов
двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
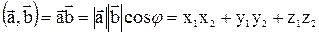
Угол между векторами  и
и  определяется по формуле
определяется по формуле
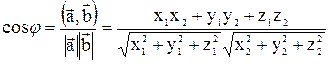
Пример 3.1. Даны векторы:
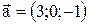
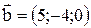
Найти:
а) векторы 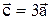 и
и  ;
;
б) длины векторов  и
и 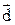 ;
;
в) скалярный квадрат вектора 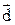 ;
;
г) скалярное произведение векторов  ;
;
д) угол меду векторами  и
и 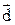 ;
;
Решение:
а) По определению  и
и  .
.
б) Найдем длины векторов:
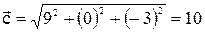
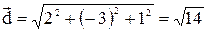
в) Скалярный квадрат вектора 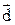 равен квадрату модуля вектора, т.е.:
равен квадрату модуля вектора, т.е.:

г) Найдем скалярное произведение:
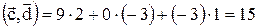
д) Найдем угол между векторами:
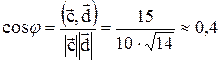
откуда 
2. ПРОВЕРКА НА БАЗИС.
Совокупность 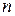 линейно независимых векторов
линейно независимых векторов  мерного пространства
мерного пространства  называются базисом.
называются базисом.
Векторы 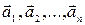 векторного пространства
векторного пространства  называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 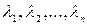 , такие что хотя бы одно из них отлично от нуля, и выполняется равенство:
, такие что хотя бы одно из них отлично от нуля, и выполняется равенство:
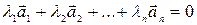 .
.
Если три вектора являются линейно независимыми (т.е. являются базисом) то они компланарны (не лежат в одной плоскости или на параллельных плоскостях).
Необходимым и достаточным условием компланарности трех векторов, заданных в декартовом базисе, является равенство нулю определителя третьего порядка, в первой строке которого записаны координаты первого вектора, во второй строке – второго, в третьей – третьего.
Пример 3.2. Проверить, образуют ли вектора 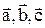 базис.
базис.
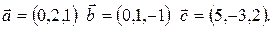 и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.
Решение.
Базис в трехмерном пространстве могут образовывать любые три линейно независимые вектора, для этого построим определитель, и убедимся что он не равен нулю.
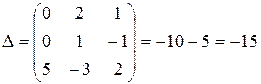
Итак, векторы 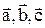 образуют базис. По теореме про линейную зависимость любых четырех векторов в трехмерном пространстве разложим вектор
образуют базис. По теореме про линейную зависимость любых четырех векторов в трехмерном пространстве разложим вектор 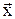 на векторах
на векторах 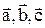 .
.

где 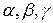 искомые координаты вектора
искомые координаты вектора 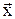 .
.
Решая полученную систему уравнений получим 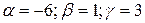 . Таким образом вектор
. Таким образом вектор 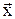 имеет в базисе
имеет в базисе 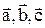 такие координаты
такие координаты 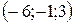 .
.
3. ЛИНЕЙНЫЙ ОПЕРАТОР
Если задан закон (правило), по которому каждому вектору 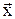 пространства
пространства 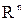 ставится в соответствие единственный вектор
ставится в соответствие единственный вектор  пространства
пространства  , то говорят, что задан оператор
, то говорят, что задан оператор  , действующий из
, действующий из 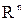 в
в  , и записывают
, и записывают  .
.
Оператор называется линейным, если для любых векторов 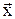 и
и 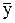 пространства
пространства 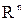 и любого числа
и любого числа  выполняются соотношения:
выполняются соотношения:
1. 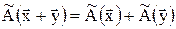 - свойство аддитивности оператора;
- свойство аддитивности оператора;
2.  - свойство однородности оператора.
- свойство однородности оператора.
Вектор  называется образом вектора
называется образом вектора 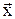 , а сам вектор
, а сам вектор 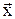 - прообразом вектора
- прообразом вектора  .
.
Каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 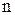 -ого порядка соответствует линейный оператор
-ого порядка соответствует линейный оператор 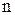 -мерного пространства.
-мерного пространства.
Связь между вектором 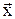 и его образом
и его образом  можно выразить в матричной форме уравнением:
можно выразить в матричной форме уравнением:
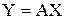 ,
,
где А – матрица линейного оператора,  ,
, 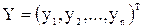 - матрицы-столбцы из координат векторов
- матрицы-столбцы из координат векторов 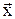 и
и  .
.
Пример 3.3. Пусть в пространстве  линейный оператор
линейный оператор  в базисе
в базисе  задан матрицей
задан матрицей  . Найти образ
. Найти образ  вектора
вектора  .
.
Решение.
По формуле 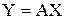 имеем:
имеем:
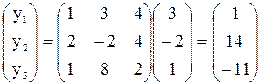
Следовательно,  .
.
4. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ
Вектор 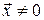 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если найдется такое число
, если найдется такое число  , что
, что
 .
.
Число  называется собственным значением оператора
называется собственным значением оператора  (матрицы А), соответствующим вектору
(матрицы А), соответствующим вектору  .
.
Равенство  можно переписать в матричной форме:
можно переписать в матричной форме:

отсюда получим:
 .
.
Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения системы необходимо и достаточно, чтобы определитель системы 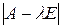 был равен нулю.
был равен нулю.
Определитель 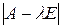 является многочленом
является многочленом 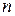 -ой степени относительно
-ой степени относительно  . Этот многочлен называется характеристическим многочленом оператора
. Этот многочлен называется характеристическим многочленом оператора  или матрицы А, а уравнение
или матрицы А, а уравнение  характеристическим уравнением оператора
характеристическим уравнением оператора  или матрицы А.
или матрицы А.
Пример 3.4. Найти собственные значения и собственные векторы линейного оператора  , заданного матрицей
, заданного матрицей  .
.
Решение. Составляем характеристическое уравнение  или
или  ,
,
откуда собственные значения линейного оператора 
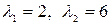 .
.
Находим собственный вектор 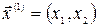 , соответствующий собственному значению
, соответствующий собственному значению  . Для этого решаем матричное уравнение:
. Для этого решаем матричное уравнение:
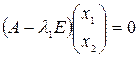 , или
, или 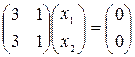 .
.
Откуда находим  или
или 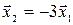 . Положив
. Положив  , получим, что векторы
, получим, что векторы  при
при  являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением  .
.
Аналогично определяем вектор 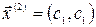 при любом
при любом  являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  с собственным значением
с собственным значением 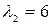 .
.
5. ИССЛЕДОВАНИЕ НА ЗНАКООПРЕДЕЛЕННОСТИ КВАДРАТИЧНОЙ ФОРМЫ
Квадратичной формой 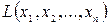 от
от 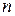 переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух переменных, взятых с некоторым коэффициентом:
переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух переменных, взятых с некоторым коэффициентом:
 .
.
Предполагается, что коэффициенты квадратичной формы 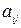 - действительные числа, причем
- действительные числа, причем 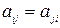 . Матрица
. Матрица 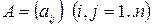 , составленная из этих коэффициентов, называется матрицей квадратичной формы.
, составленная из этих коэффициентов, называется матрицей квадратичной формы.
В матричной записи квадратичная форма имеет вид:
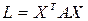
где  - матрица-столбец переменных.
- матрица-столбец переменных.
Теорема. Для того чтобы квадратичная форма 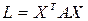 была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения  матрицы А были положительны (отрицательны).
матрицы А были положительны (отрицательны).
Если собственные значения  разных знаков то знакоопределённость квадратичной формы установить нельзя.
разных знаков то знакоопределённость квадратичной формы установить нельзя.
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 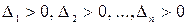 , где:
, где:
 ,
, 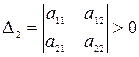 , …,
, …, 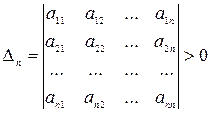
Для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка:
 ,
,  , …,
, …, 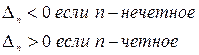 .
.
Если не один из критериев не выполняется, то знакоопределённость матрицы не устанавливается.
Пример 3.5. Проверить знакоопределенность квадратичной формы
a) 
б) 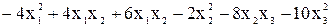
Решение:
а) При помощи собственных значений:
Матрица  квадратичной формы имеет вид
квадратичной формы имеет вид  . Для матрицы А характеристическое уравнение имеет вид:
. Для матрицы А характеристическое уравнение имеет вид:
 или
или  .
.
Решая уравнение найдем 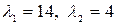 . Так как корни характеристического уравнения матрицы А положительны, но квадратичная форма положительно определенная.
. Так как корни характеристического уравнения матрицы А положительны, но квадратичная форма положительно определенная.
При помощи критерия Сильвестра:
Так как главные миноры матрицы А

положительны, то по критерию Сильвестра данная квадратичная форма положительно определенная.
б) Матрица квадратичной формы имеет вид  . Поскольку при нахождении собственных значений получим уравнение третей степени, для определения знакоопределенности воспользуемся для удобства лишь критерием Сильвестра.
. Поскольку при нахождении собственных значений получим уравнение третей степени, для определения знакоопределенности воспользуемся для удобства лишь критерием Сильвестра.
Главные миноры матрицы А:
 .
.
Так как знаки миноров чередуются начиная со знака «минус», то это означает что квадратичная форма отрицательно определена.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 11930; Нарушение авторских прав?; Мы поможем в написании вашей работы!