Проверка функции на непрерывность

Эквивалентные бесконечно малые функции.

Замечательные пределы.

Предел функции.

ТЕМА 4. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ.

1. ПРЕДЕЛ ФУНКЦИИ

Определение. Если по некоторому закону каждому натуральному числу 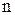поставлено в соответствие вполне определенное число 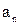, то говорят, что задана числовая последовательность :

.

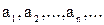Другими словами, числовая последовательность – это функция натурального аргумента: .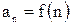

Числа 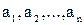называются членами последовательности, а число 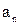- общим, или 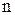-м членом данной последовательности.

Определение. Число А называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного 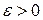, найдется такой номер 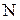(зависящий от 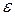, 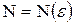), что для всех членов последовательности с номерами 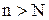верно неравенство

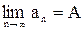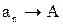Предел числовой последовательности обозначается или при .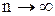

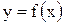Определение. Число называется пределом функции при 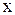, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 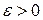, найдется такое положительное число 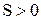(зависящее от 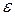, ), что для всех 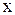таких, что 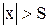, верно неравенство:

.

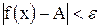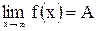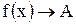Этот предел функции обозначается или при .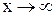

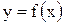Определение. Число называется пределом функции при 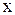, стремящемся к 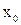(или в точке 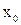), если для любого, даже сколь угодно малого положительного числа 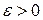, найдется такое положительное число 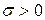(зависящее от 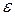, 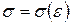), что для всех 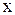, не равных 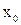и удовлетворяющих условию

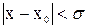
верно неравенство:

.

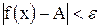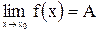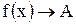Этот предел функции обозначается или при .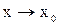

Пример 6.1. Найти предел функции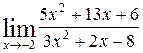

Решение: Имеем неопределенность вида 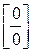. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель 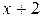, который при 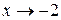не равен нулю. В результате неопределенность будет раскрыта.

Пример 6.2. Найти предел функции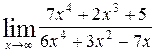

Решение: Имеем неопределенность вида 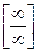. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.

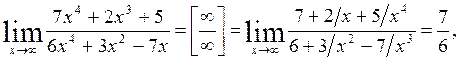
или

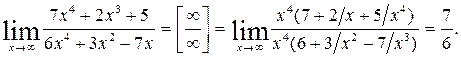
Пример 6.3. Найти предел функции

Решение: Имеем неопределенность вида 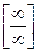. Раскрываем ее аналогично тому как это сделано в примере 6.2.

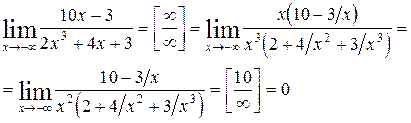
Пример 6.4. Найти предел функции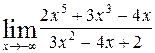

Решение: Имеем неопределенность вида 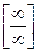. Раскрываем ее аналогично тому как это сделано в примере 2.

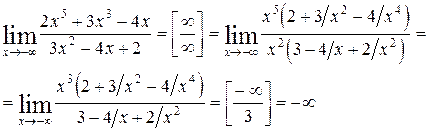
Пример 6.5. Найти предел функции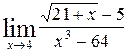

Решение: Имеем неопределенность вида 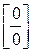. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель 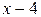, который при 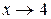не равен нулю. В результате неопределенность будет раскрыта.

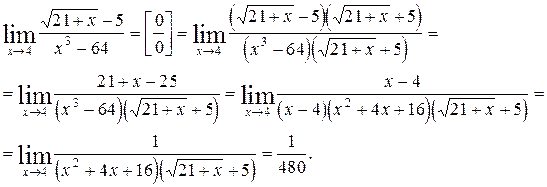
2. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Первым замечательным пределом называется:

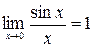
Число (вторым замечательным пределом) называется предел числовой последовательности:

.

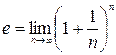Пример 6.6 Найти предел функции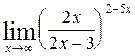

Решение: Имеем неопределенность вида 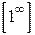. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом .

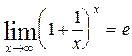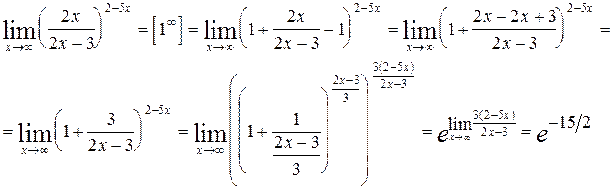
Пример 6.7. Найти предел функции

Решение: В данном примере при выяснении вида неопределенности видим, что таковой не имеется.

Имеем 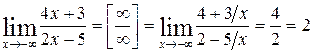, тогда

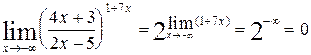
3. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ

Определение.

Таблица эквивалентных бесконечно малых величин.

Пример 6.8. Найти предел, используя эквивалентные бесконечно малые функции

Решение: Имеем неопределенность вида 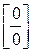. Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как и , то

4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Функция 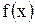называется непрерывной в точке 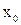, если она удовлетворяет следующим трем условиям:

1) определена в точке 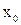(т.е. существует ;

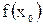2) имеет конечный предел функции при ;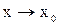

3) этот предел равен значению функции в точке .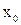

Точка 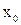называется точкой разрыва функции 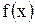, если эта функция в данной точке не является непрерывной. Различают точки разрыва: первого рода (когда существуют конечные односторонние пределы функции слева и справа при 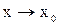, не равные друг другу) и второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует).

К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при 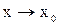существует, но не равнее значению функции в этой точке.

Пример 6.9. Исследовать данную функцию на непрерывность и построить ее график

Решение: Функция является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах 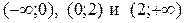, где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках 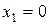и .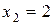

Для точки 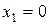имеем:

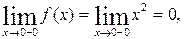
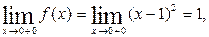
Так как 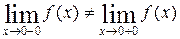, то функция в точке 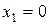имеет разрыв первого рода.

Для точки 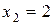находим:

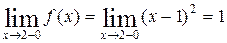
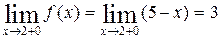
Так как , то функция в точке 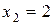имеет разрыв первого рода.

График данной функции изображен на рис. 1.

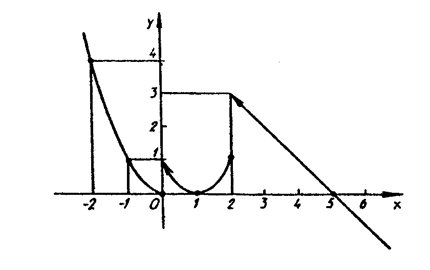Рис. 3.

Пример 6.10. Исследовать данную функцию на непрерывность в указанных точках

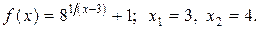
Решение:

Для точки имеем:

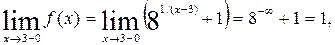
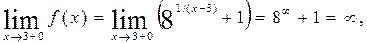
т.е. в точке функция имеет разрыв второго рода (терпит бесконечный разрыв).

Для точки 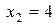имеем:

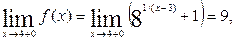
Следовательно, в точке 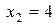функция непрерывна.

Дата добавления: 2014-01-06