
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование тригонометрических функций
|
|
|
|
Интегрирование иррациональных функций.
Интегрирование простейших рациональных дробей.
Метод интегрирования по частям.
Метод замены переменной.
Интегралы основных элементарных функций.
Свойства неопределенного интеграла.
Первообразная функция и неопределенный интеграл.
ТЕМА 6. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
1. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Определение. Функция 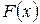 называется первообразной функцией для функции
называется первообразной функцией для функции 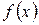 на промежутке
на промежутке 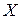 , если в каждой точке
, если в каждой точке 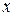 этого промежутка
этого промежутка 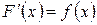 .
.
Например, 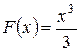 является первообразной для функции
является первообразной для функции 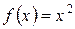 , так как
, так как 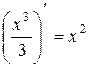 .
.
По геометрическому смыслу производной 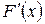 есть угловой коэффициент касательной к кривой
есть угловой коэффициент касательной к кривой  в точке с абсциссой
в точке с абсциссой 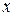 . Геометрически найти первообразную для
. Геометрически найти первообразную для 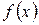 - значит найти такую кривую
- значит найти такую кривую  , что угловой коэффициент касательной к ней в произвольной точке
, что угловой коэффициент касательной к ней в произвольной точке 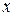 равен значению
равен значению 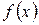 заданной функции в этой точке.
заданной функции в этой точке.
Теорема. Если 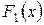 и
и 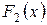 - первообразные для функции
- первообразные для функции 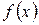 на некотором промежутке
на некотором промежутке 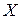 , то найдется такое число
, то найдется такое число 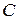 , что будет справедливо равенство:
, что будет справедливо равенство:
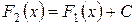
Из данной теоремы следует, что, если 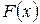 - первообразная для функции
- первообразная для функции 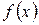 , то выражение вида
, то выражение вида 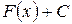 , где
, где 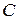 - произвольное число, задет все возможные первообразные для
- произвольное число, задет все возможные первообразные для 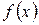 .
.
Определение. Совокупность всех первообразных для функции 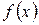 на промежутке
на промежутке 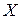 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 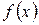 и обозначается
и обозначается 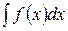 , где
, где 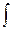 - знак интеграла,
- знак интеграла, 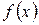 - подынтегральная функция,
- подынтегральная функция, 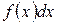 - подынтегральное выражение. Таким образом:
- подынтегральное выражение. Таким образом:
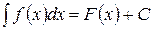
где 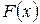 - некоторая первообразная для
- некоторая первообразная для 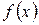 ,
, 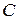 - произвольная постоянная.
- произвольная постоянная.
Например, поскольку 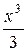 - первообразная для функции
- первообразная для функции 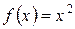 , то
, то 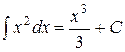 .
.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Пример 10.1. Известно значение интеграла  . Найти функцию
. Найти функцию 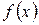 .
.
Решение.
Поскольку 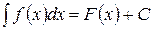 , где
, где 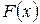 - первообразная функции
- первообразная функции 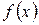 , то по определению первообразной
, то по определению первообразной 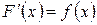 для того чтобы найти
для того чтобы найти 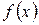 необходимо взять производную от выражения
необходимо взять производную от выражения 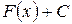 .
.
Таким образом:
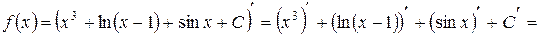
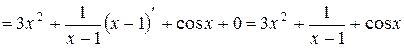
т.е.
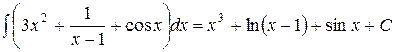
2. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ИНТЕГРАЛЫ ОТ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
Основные свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.
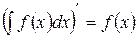
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.
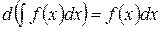
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
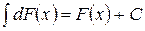
где С – произвольное число.
4. Постоянный множитель можно выносить за знак интеграла, т.е.
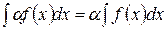
где 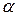 - некоторое число.
- некоторое число.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
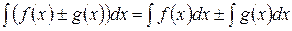
3. ТАБЛИЧНЫЕ ИНТЕГРАЛЫ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
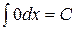
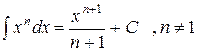
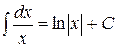
для произвольного интервала, не содержащего точки 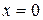 ,
,
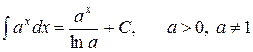
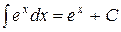
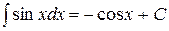
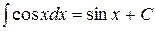
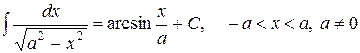
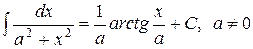
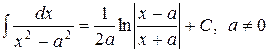
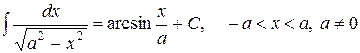
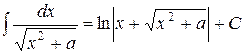
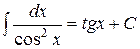
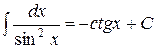
Пример 10.2. Найти интегралы:
а) 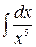 б)
б) 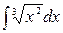 в)
в) 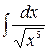
РЕШЕНИЕ:
Во всех трех случаях нам придется воспользоваться одним и тем же табличным интегралом 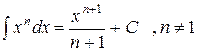
а) при 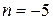
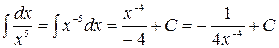 ;
;
б) при 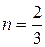
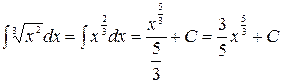 ;
;
в) при 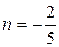
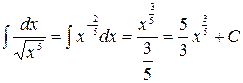 ;
;
Пример 10.3. Найти интегралы:
а) 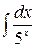 ; б)
; б) 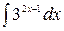 в)
в) 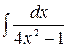 г)
г) 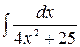 д)
д) 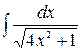
РЕШЕНИЕ:
а) Используем формулу 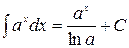 , где
, где 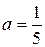 :
:
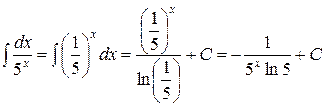
б) 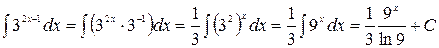
в) Поскольку 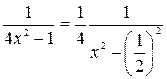 , то воспользуемся формулой
, то воспользуемся формулой 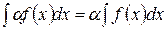 , а потом формулой
, а потом формулой 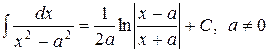 :
:
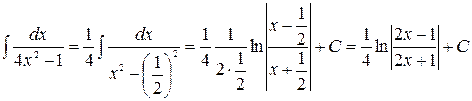
г) Так как 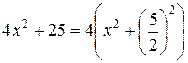 , то используя формулу
, то используя формулу 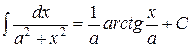 , где
, где 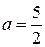 , получаем:
, получаем:
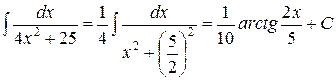
д) Так как 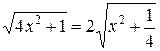 , то используя формулу
, то используя формулу 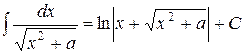 при
при 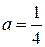 получим:
получим:
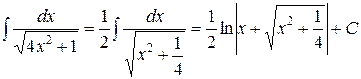 .
.
4. МЕТОД РАЗЛОЖЕНИЯ
Метод интегрирования, основанный на применении свойств 4 и 5 из пункта 2, называется методом разложения. Суть его заключается в следующем: вначале производится преобразование подынтегральной функции (при помощи формул сокращенного умножения, тригонометрических тождеств и т.п.) до тех пор пока не будут получены табличные интегралы описанные выше. В случае если табличные интегралы путем таких преобразований получить не удается, то этот метод не применим для интегрирования, и необходима применять один из методов который будет описан в следующих пунктах.
Пример 10.4. Используя метод разложения, найти интегралы:
а) 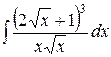 ; б)
; б) 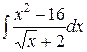 ; в)
; в) 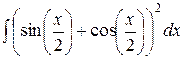
г) 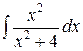
РЕШЕНИЕ:
а) 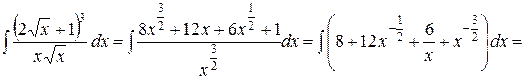
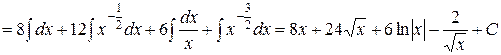
б) 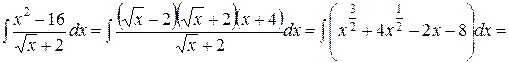
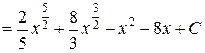
в) 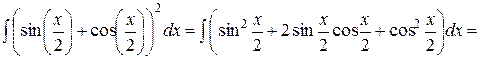
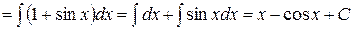
5. МЕТОД ЗАМЕНЫ ПЕРЕМЕННЫХ
Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой:
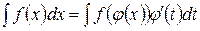 ,
,
где 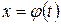 - функция, дифференцируемая на рассматриваемом промежутке.
- функция, дифференцируемая на рассматриваемом промежутке.
Удачная замена переменной позволяет упростить исходный интеграл, а в простейших случаях свести его к табличному.
Теорема. Пусть 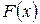 некоторая первообразная для функции
некоторая первообразная для функции 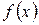 . Тогда
. Тогда
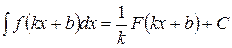
где 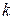 и
и 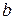 - некоторые числа,
- некоторые числа, 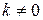 .
.
Пример 10.5. Найти интегралы:
а) 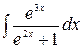 б)
б)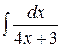 в)
в) 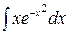
РЕШЕНИЕ:
а) Сделаем замену 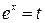 . Тогда
. Тогда 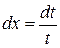 и
и 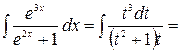
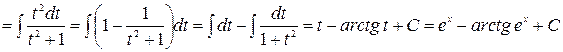
б) Делаем замену (линейную подстановку) 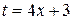 ,
, 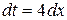 следовательно
следовательно 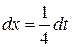 . Тогда:
. Тогда:
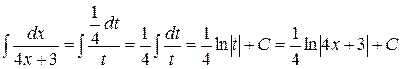
в) Сделаем замену 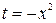 , тогда
, тогда 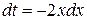 , т.е.
, т.е.  , таким образом:
, таким образом:
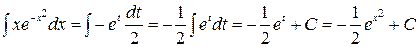
6. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Пусть 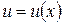 и
и 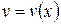 - дифференцируемые функции. По свойству дифференциала:
- дифференцируемые функции. По свойству дифференциала:
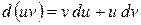
или

Интегрируя левую и правую части последнего равенства получаем:
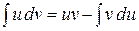 .
.
Эта формула называется формулой интегрирования по частям для неопределенного интеграла.
Можно указать следующие типы интегралов, для нахождения которых используется формула интегрирования по частям:
1. 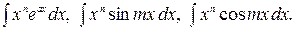
2. 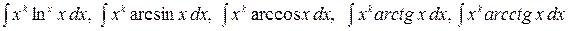
где 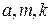 - действительные числа
- действительные числа 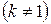 ,
, 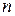 - положительное число.
- положительное число.
Для нахождения интегралов из первой группы формулу интегрирования по частям придется применить 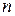 раз (при первом применении полагают
раз (при первом применении полагают 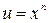 , остальные сомножители подынтегрального выражения задают
, остальные сомножители подынтегрального выражения задают 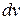 ), пока степень
), пока степень 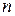 переменной
переменной 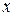 не станет равной нулю, а сам интеграл табличным (см. пример ниже). Для нахождения интегралов второй группы полагают
не станет равной нулю, а сам интеграл табличным (см. пример ниже). Для нахождения интегралов второй группы полагают 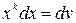 (оставшиеся сомножители подынтегрального выражения задают выражение для
(оставшиеся сомножители подынтегрального выражения задают выражение для 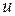 ).
).
На практике метод интегрирования по частям часто комбинируется с другими методами интегрирования.
Пример 10.6. Найти интегралы:
а)  б)
б) 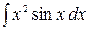 в)
в) 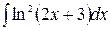
РЕШЕНИЕ:
а) «Препятствием» к нахождению данного интеграла является присутствие сомножителя 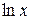 в записи подынтегральной функции. Устранить его в данном случае можно интегрированием по частям. Полагаем
в записи подынтегральной функции. Устранить его в данном случае можно интегрированием по частям. Полагаем 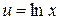 , тогда
, тогда 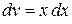 . Тогда
. Тогда 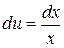 и
и 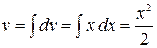 . Используем формулу интегрирования по частям:
. Используем формулу интегрирования по частям:
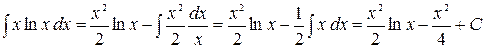
б) Положим 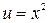 ,
, 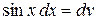 , тогда
, тогда 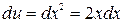 и
и 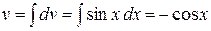 . Применяя формулу интегрирования по частям получим:
. Применяя формулу интегрирования по частям получим:
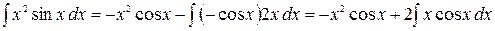
Возникший интеграл не является табличным, однако видно, что мы на правильном пути: по сравнению с исходным интегралом степень переменной 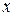 в подынтегральном выражении уменьшилась на единицу, при этом второй сомножитель
в подынтегральном выражении уменьшилась на единицу, при этом второй сомножитель 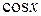 того же типа, что и в исходном интеграле. Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Положим
того же типа, что и в исходном интеграле. Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Положим 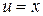 ,
, 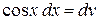 , тогда
, тогда 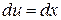 ,
, 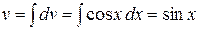 и:
и:
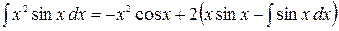 =
=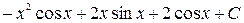
в) Выполним сначала замену переменной: положим 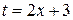 , тогда
, тогда 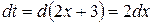 и
и 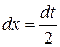 , следовательно:
, следовательно:
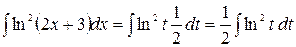
Пусть 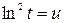 ,
, 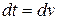 , тогда
, тогда 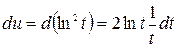 ,
,  , применяя формулу интегрирования по частям получаем:
, применяя формулу интегрирования по частям получаем:
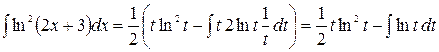 .
.
Полагая в формуле интегрирования по частям 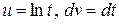 получаем
получаем 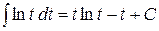 . Окончательно имеем:
. Окончательно имеем:
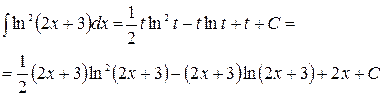
7. ИНТЕГРИВРОВАНИЕ ПРОСТЕЙШИХ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Многочленом степени 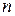 называется выражение вида
называется выражение вида 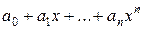 , где
, где 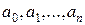 - действительные числа
- действительные числа 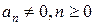 . Например
. Например 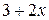 - многочлен первой степени,
- многочлен первой степени, 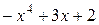 - многочлен четвертой степени и т.д. Рациональной дробью называется отношение двух многочленов. Например,
- многочлен четвертой степени и т.д. Рациональной дробью называется отношение двух многочленов. Например, 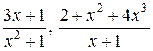 - рациональные дроби.
- рациональные дроби.
Достаточно рассмотреть правильные дроби, т.е. такие, у которых степень числителя меньше степени знаменателя. В самом деле, если это не так, то, используя алгоритм деления многочленов «углом» можно представить исходную дробь в виде суммы многочлена и правильной дроби.
Если степень знаменателя равна 1, то искомый интеграл имеет вид 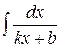 , и для его нахождения достаточно воспользоваться формулой
, и для его нахождения достаточно воспользоваться формулой 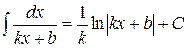 или заменой переменной
или заменой переменной 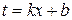 .
.
Пусть степень знаменателя равна 1, т.е. искомым является интеграл вида:
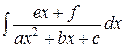 ,
,
где 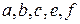 - действительные числа,
- действительные числа, 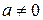 .
.
Рассмотрим важный частный случай:
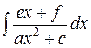
а затем укажем, как общий случай свести к данному. Если 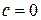 , то интеграл представляет собой сумму двух табличных интегралов (см. метод разложения). Пусть
, то интеграл представляет собой сумму двух табличных интегралов (см. метод разложения). Пусть 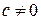 , тогда для нахождения этого интеграла достаточно найти интегралы
, тогда для нахождения этого интеграла достаточно найти интегралы
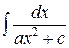
и
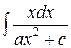 .
.
Первый сводится (вынесением множителя 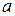 ) к табличному интегралу (см. пример 10.3 в,г).
) к табличному интегралу (см. пример 10.3 в,г).
Для нахождения второго интеграла используем замну переменной 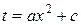 . Тогда
. Тогда 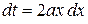 ,
, 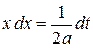 . Получаем:
. Получаем:
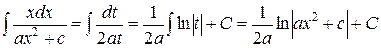 .
.
Возвращаясь к интегралу 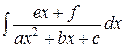 , заметим, что его можно привести к виду
, заметим, что его можно привести к виду 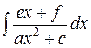 , если сначала выделить полный квадрат в знаменателе подынтегральной функции, а затем использовать соответствующую (линейную) замену переменной.
, если сначала выделить полный квадрат в знаменателе подынтегральной функции, а затем использовать соответствующую (линейную) замену переменной.
Пример 10.7. Найти интегралы:
а) 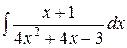 б)
б) 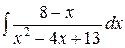
РЕШЕНИЕ:
а) Выделим полный квадрат в знаменателе 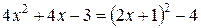 , сделаем замену
, сделаем замену  , тогда
, тогда 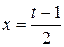 ,
, 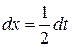 , получим:
, получим:
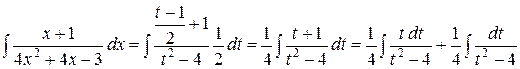
Для нахождения первого интеграла воспользуемся формулой описанной выше 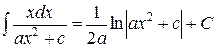 при
при 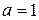 ,
, 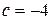 . Второй интеграл табличный.
. Второй интеграл табличный.
Таким образом имеем:
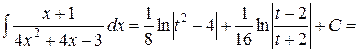
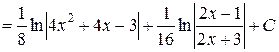
б) Так как  , то положим
, то положим 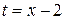 , тогда,
, тогда, 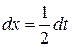 ,
, 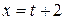 и получим:
и получим:
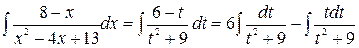
Первый из интегралов табличный, для нахождения второго воспользуемся методом, описанным в предыдущем примере. Тогда получим:
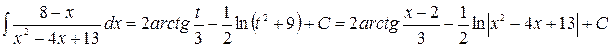
Рассмотренный прием интегрирования правильных дробей, знаменатель которых имеет вторую степень (выделение полного квадрата с последующей заменой переменной) имеет существенный недостаток: он не обобщается на случаи, когда степень знаменателя больше двух. Поэтому в этом случае применяется метод неопределенных коэффициентов.
В общем случае можно доказать, что если подынтегральная функция 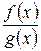 - правильная дробь, знаменатель
- правильная дробь, знаменатель 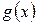 которой – многочлен степени
которой – многочлен степени 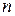 , имеющий
, имеющий 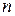 попарно различных действительных корней
попарно различных действительных корней 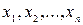 , то существует представление подынтегральной функции в виде:
, то существует представление подынтегральной функции в виде:
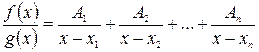
Пример 10.8. Найти интеграл: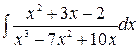
РЕШЕНИЕ:
Так как 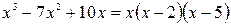 , то:
, то:
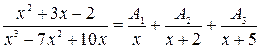
Из последнего равенства найдем постоянные 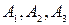 . Приводя дроби правой части к общему знаменателю приходим к равенству:
. Приводя дроби правой части к общему знаменателю приходим к равенству:
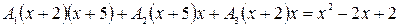
Если 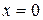 , то имеем
, то имеем 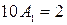 и
и 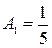 ;
;
если 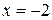 , то имеем
, то имеем 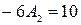 и
и 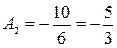 ;
;
если 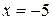 , то имеем
, то имеем 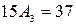 и
и 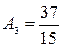 .
.
Тогда:
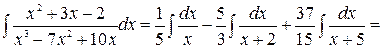
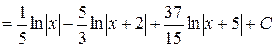 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1051; Нарушение авторских прав?; Мы поможем в написании вашей работы!