
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородные уравнения
|
|
|
|
Определение. Уравнения (2.2) или (2.3) называются однородными, если  есть однородная функция нулевого измерения:
есть однородная функция нулевого измерения:
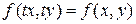 , (3.5)
, (3.5)
или функции  и
и 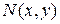 являются однородными одного измерения:
являются однородными одного измерения:
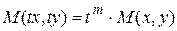 ,
,  . (3.6)
. (3.6)
Однородное уравнение (2.2) всегда можно представить в виде:
 . (3.7)
. (3.7)
Любой из подстановок -  , или
, или  - однородное уравнение сводится к уравнению с разделяющимися переменными. Например, вводя новую искомую функцию
- однородное уравнение сводится к уравнению с разделяющимися переменными. Например, вводя новую искомую функцию  , сведем (3.7) к уравнению
, сведем (3.7) к уравнению
 , (3.8)
, (3.8)
в котором переменные разделяются. Если  есть корень уравнения
есть корень уравнения 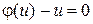 , то решением однородного уравнения будет
, то решением однородного уравнения будет  или
или 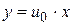 (прямая, проходящая через начало координат).
(прямая, проходящая через начало координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (3.7). Можно сразу выполнять подстановку 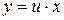 (или
(или 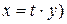 .
.
Пример 1. Решить уравнение 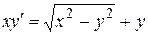 .
.
Решение. Имеем однородное уравнение (заменяя в уравнении x и y на tx, ty приходим к исходному уравнению: 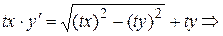
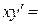
 ; иначе, уравнение приводится к виду
; иначе, уравнение приводится к виду 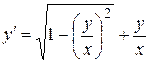
 . Положим
. Положим 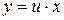 . Тогда
. Тогда  . Подставим в уравнение, получим:
. Подставим в уравнение, получим: 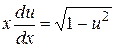 . Разделим переменные:
. Разделим переменные:  . Отсюда интегрированием функций находим
. Отсюда интегрированием функций находим  или
или  . Подставляя
. Подставляя  , после преобразования получим общее решение
, после преобразования получим общее решение 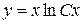 . При разделении переменных обе части уравнения делили на произведение
. При разделении переменных обе части уравнения делили на произведение  , поэтому могли потерять решения, которые обращают в нуль это произведение. Положим
, поэтому могли потерять решения, которые обращают в нуль это произведение. Положим  (
( - см. область определения уравнения). Из этого уравнения находим
- см. область определения уравнения). Из этого уравнения находим 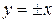 . Проверка показывает, что и
. Проверка показывает, что и  и
и  – решения данного уравнения.
– решения данного уравнения.


1°. Линейные уравнения. Линейным дифференциальным уравнением называется линейное относительно неизвестной функции и ее производной уравнение:
 , (3.10)
, (3.10)
где 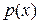 и
и  - заданные функции от
- заданные функции от 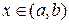 , непрерывные в области интегрирования уравнения (3.10). Через каждую точку
, непрерывные в области интегрирования уравнения (3.10). Через каждую точку 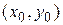 полосы
полосы  ,
,  проходит одна, и только одна, интегральная кривая уравнения (3.10), определенная во всем интервале
проходит одна, и только одна, интегральная кривая уравнения (3.10), определенная во всем интервале 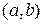 . Всякое решение линейного уравнения есть частное, так что особых решений оно не имеет.
. Всякое решение линейного уравнения есть частное, так что особых решений оно не имеет.
Если  , то уравнение (3.10) называется линейным однородным:
, то уравнение (3.10) называется линейным однородным:
 . (3.11)
. (3.11)
Оно является уравнением с разделяющимися переменными и имеет общее решение
 . (3.12)
. (3.12)
Все решения линейного однородного уравнения (3.11) содержатся в формуле (3.12) его общего решения. Общее решение неоднородного линейного уравнения (3.10) может быть найдено несколькими способами; здесь рассмотрим два из них.
а) метод подстановки. Положим 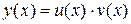 . Тогда уравнение (3.10) приводится к виду
. Тогда уравнение (3.10) приводится к виду
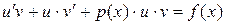 . (3.13)
. (3.13)
Выберем функции 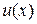 и
и  так, чтобы сумма
так, чтобы сумма  обратилась в ноль. Так как
обратилась в ноль. Так как 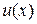 не равна тождественно нулю (
не равна тождественно нулю ( не является решением уравнения (3.10)), то должно быть
не является решением уравнения (3.10)), то должно быть
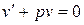 (3.14)
(3.14)
- для определения функции  получили уравнение с разделяющимися переменными. Выбрав какое – либо частное решение
получили уравнение с разделяющимися переменными. Выбрав какое – либо частное решение  , подставим его в (3.13); для определения функции
, подставим его в (3.13); для определения функции 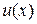 получим уравнение с разделяющимися переменными
получим уравнение с разделяющимися переменными
 . (3.15)
. (3.15)
Решая уравнение (3.15), найдем его общее решение 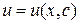 . Перемножая найденные функции
. Перемножая найденные функции  и
и 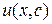 , получим общее решение уравнения (3.10):
, получим общее решение уравнения (3.10):
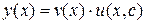 .
.
Пример 1. Решить уравнение  . Выделить частное решение, проходящее через точку
. Выделить частное решение, проходящее через точку  .
.
Решение. Ищем общее решение уравнения в виде 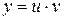 . Подставляя
. Подставляя 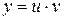 и
и  в уравнение, получим:
в уравнение, получим: 
 , или
, или 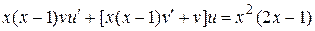 (*). Функцию
(*). Функцию 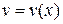 найдем из условия
найдем из условия 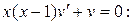
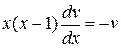 ,
, 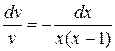 .
.
Интегрируем уравнение 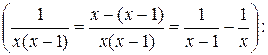
 . Возьмем частное решение
. Возьмем частное решение  . Подставляя его в (*), получим уравнение
. Подставляя его в (*), получим уравнение 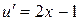 , из которого интегрированием находим функцию
, из которого интегрированием находим функцию 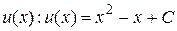 . Общее решение исходного уравнения
. Общее решение исходного уравнения 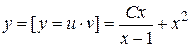 .
.
Чтобы выделить нужную интегральную кривую, подставим в найденное решение  :
:  , откуда С = 0; решением поставленной задачи Коши служит парабола
, откуда С = 0; решением поставленной задачи Коши служит парабола 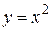 .
.
Пример 2. Решить уравнение 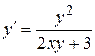 .
.
Решение. Перепишем уравнение в виде  - оно линейно относительно x и
- оно линейно относительно x и  . Решим его методом подстановки. Полагаем
. Решим его методом подстановки. Полагаем  , тогда
, тогда 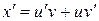 и после подстановки x и
и после подстановки x и 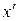 в уравнение, оно приводится к виду:
в уравнение, оно приводится к виду:  (*). Функцию
(*). Функцию 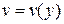 определяем из уравнения
определяем из уравнения 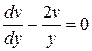 . Из его общего решения
. Из его общего решения 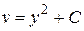 выберем, например, частное
выберем, например, частное 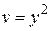 и подставим его в (*); получим
и подставим его в (*); получим  или
или  . Общее решение этого уравнения:
. Общее решение этого уравнения:  . Перемножая
. Перемножая 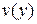 и
и 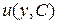 , получим общее решение данного уравнения
, получим общее решение данного уравнения 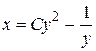 .
.




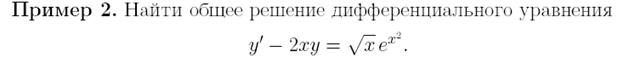









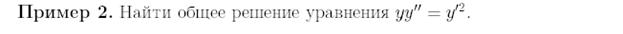

Уравнение вида
 (5.11)
(5.11)
допускает понижение порядка на единицу, если ввести новую искомую функцию:  и принять y за независимую переменную
и принять y за независимую переменную  . При этом производные
. При этом производные 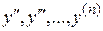 преобразуются так:
преобразуются так:
 ;
;
 (5.12)
(5.12)
Пример 4. Решить уравнение 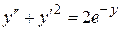 .
.
Решение. Уравнение не содержит независимое переменное x. Полагая 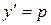 ,
, 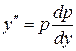 , приходим к уравнению первого порядка
, приходим к уравнению первого порядка 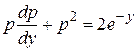 - уравнению Бернулли, решаемому, например, с помощью подстановки
- уравнению Бернулли, решаемому, например, с помощью подстановки 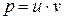 :
:
 , откуда
, откуда  . Заменяя здесь p на
. Заменяя здесь p на  , разделяя переменные и интегрируя, будем иметь
, разделяя переменные и интегрируя, будем иметь  . Подставляя
. Подставляя
y = C в уравнение, убеждаемся, что y = C не является его решением.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1413; Нарушение авторских прав?; Мы поможем в написании вашей работы!