
- Р Р‡.МессенРТвЂВВжер
- ВКонтакте
- РћРТвЂВВнокласснРСвЂВВРєРСвЂВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математичний опис імпульсних систем з АІМ
Для математичного опису ІС всі сигнали, в тому числі в неперервній частині, розглядаються в дискретні моменти часу 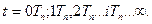 Неперервні сигнали подаються у вигляді решітчастих функцій (рис.3.6):
Неперервні сигнали подаються у вигляді решітчастих функцій (рис.3.6):
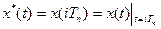 (3.9)
(3.9)
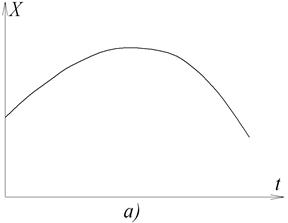
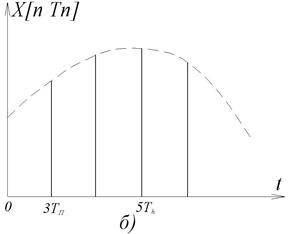
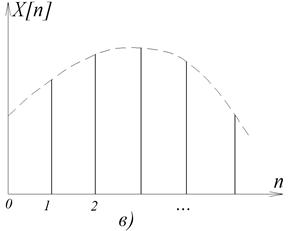
Рис.3.6. Решітчасті функції.
а – неперервний сигнал; б, в – форми представлення решітчастих функцій
Між дискретними значеннями аргументу решітчаста функція дорівнює нулю, а неперервний сигнал є обвідною для решітчастої функції. Послідовність неодиночних імпульсів, які утворюють решітчасту функцію на інтервалі 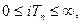 можна подати у вигляді нескінченного ряду:
можна подати у вигляді нескінченного ряду:
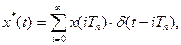 (3.10)
(3.10)
де: 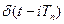 - зміщена
- зміщена 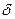 - функція, яка існує лише в моменти часу t=iTn і дорівнює нулю при всіх інших значеннях t. Для решітчастої функції існує дискретне перетворення Лапласа:
- функція, яка існує лише в моменти часу t=iTn і дорівнює нулю при всіх інших значеннях t. Для решітчастої функції існує дискретне перетворення Лапласа:
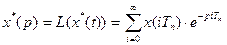 (3.11)
(3.11)
Вираз (3.11) отримано з урахуванням того, що зображення суми оригіналів дорівнює сумі їх зображень, а зображення зміщеної 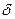 - функції дорівнює
- функції дорівнює 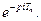 Дискретне перетворення Лапласа включає трансцендентний множник
Дискретне перетворення Лапласа включає трансцендентний множник  , тому зображення Х*(р) та передаточні функції стають ірраціональними функціями аргументу р, що утруднює їх використання. Для отримання передаточних функцій в дрібно-раціональній формі (як для неперервних систем) замінюють аргумент
, тому зображення Х*(р) та передаточні функції стають ірраціональними функціями аргументу р, що утруднює їх використання. Для отримання передаточних функцій в дрібно-раціональній формі (як для неперервних систем) замінюють аргумент
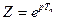 (3.12)
(3.12)
і отримують зручне для використання Z – перетворення решітчастої функції:
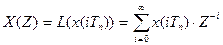 (3.13)
(3.13)
В табл. 3.3 наведені Z – зображення для деяких функцій часу.
Таблиця 3.3
Z – зображення функцій часу
| № п/п | X(t)
(t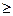 0) 0)
| X(iTn) | X(p) | X(Z) |
| 1. | 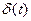
| 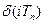
| ||
| 2. | 1(t) | 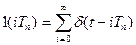
| 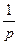
| 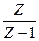
|
| 3. | t | iTn | 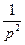
| 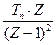
|
| 4. | t2 | (iTn)2 | 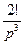
| 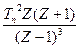
|
| 5. | e -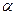 t t
| 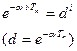
| 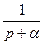
| 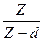
|
Зручність Z – перетворення полягає в тому, що сама форма запису дає простий спосіб прямого та зворотного перетворення:
- для знаходження Z – перетворення за відомою функцією часу необхідно кожне дискретне значення Х(іТп) помножити на Z-i, а потім згорнути отриманий степеневий ряд в кінцеву суму;
- для знаходження оригіналу за відомим зображенням Х(Z) необхідно зображення подати у вигляді степеневого ряду за спадними степенями Z-i, а отримані при цьому числові коефіцієнти ряду і є дискретними значеннями Х(іТп) сигналу Х(t).
Z – перетворення має властивості, аналогічні властивостям звичайного перетворення Лапласа:
- лінійність:
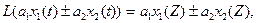 (3.14)
(3.14)
- теорема про початкове значення оригіналу:
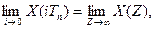 (3.15)
(3.15)
- теорема про кінцеве значення оригіналу:
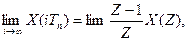 (3.16)
(3.16)
- теорема про зміщення аргументу оригінала (теорема запізнювання):
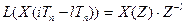 (3.17)
(3.17)
Для типового імпульсного ланцюга (рис.3.7) вхідний та вихідний сигнали розглядаються в дискретні моменти часу іТп (на виході неперервної частини показано фіктивний квантуватель, який працює синхронно з вхідним). Передаточна функція ланцюга буде:
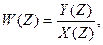 (3.18)
(3.18)
яка зв’язана з ваговою функцією W(t) неперервної частини за допомогою Z – перетворення:
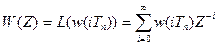 (3.19)
(3.19)

Рис.3.7 Типовий імпульсний ланцюг
Передаточну функцію W(Z) можна визначити за таблицями у відповідності до W(p). Тоді умовно запишемо:
W(Z)=L(W(p)) (3.20)
В типовому ланцюзі після “ключа” може стояти фіксатор, тоді:
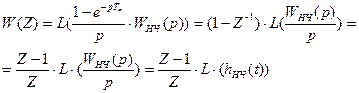 (3.21)
(3.21)
Наведені формули точні, але незручні для реальних систем високих порядків. В практичних розрахунках використовують наближені методи переходу від W(p) до W(Z), які засновані на заміні похідної за часом, що є в рівнянні неперервної частини так званою першою різницею:
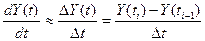 (3.22)
(3.22)
Підставляючи цю різницю в рівняння інтегратора
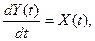 (3.23)
(3.23)
отримаємо різницеве рівняння інтегратора:
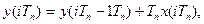 (3.24)
(3.24)
яке в Z – перетворенні буде:
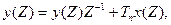 (3.25)
(3.25)
звідки дискретна передаточна функція інтегратора буде:
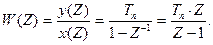 (3.26)
(3.26)
Враховуючи, що звичайна передаточна функція інтегратора: W(p)=1/p, отримують наближену формулу для переходу від W(p) до W(Z):
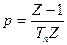 (3.27)
(3.27)
Використовується також більш точний перехід від неперервної частини до дискретної (підстановка Тастона):
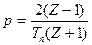 (3.28)
(3.28)
Формула (3.27) відповідає наближеному чисельному інтегруванню за методом прямокутників, формула (3.28) – інтегруванню за методом трапецій.
Наближені методи переходу дають найкращі результати при достатньо великій частоті дискретності 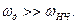 Тоді частотні властивості імпульсної ланки еквівалентні властивостям неперервної частини з амплітудно-фазовою характеристикою
Тоді частотні властивості імпульсної ланки еквівалентні властивостям неперервної частини з амплітудно-фазовою характеристикою  , коли найбільша постійна часу неперервної частини більша Тп.
, коли найбільша постійна часу неперервної частини більша Тп.
Частотні властивості імпульсних систем значно відрізняються від властивостей неперервних систем. Квантуватель за часом, або ідеальний імпульсний елемент, можна розглядати як генератор додаткових гармонік, частота яких дорівнює частоті дискретизації  . Спектр
. Спектр 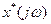 сигналу х*(t), квантованого за АІМ, дорівнює сумі зміщених спектрів неперервного вхідного сигналу х(t):
сигналу х*(t), квантованого за АІМ, дорівнює сумі зміщених спектрів неперервного вхідного сигналу х(t):
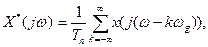 (3.29)
(3.29)
де: 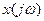 - спектр вхідного квантованого сигналу (рис.3.8,а).
- спектр вхідного квантованого сигналу (рис.3.8,а).
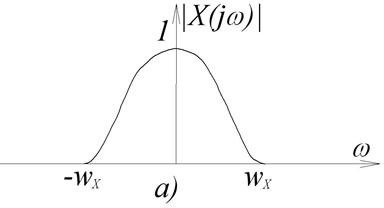
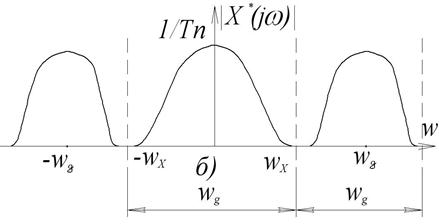
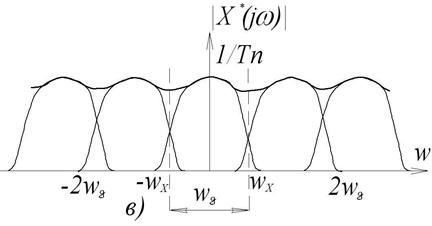
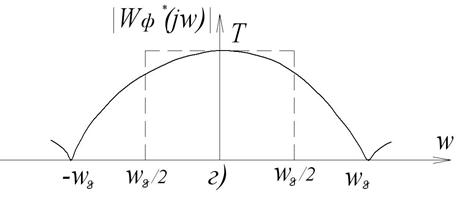
Рис.3.8. Амплітудні спектри сигналів імпульсної системи
При квантуванні амплітуда всіх гармонік зменшується в Тп разів, тобто імпульсний елемент еквівалентний без інерційній ланці з передаточним коефіцієнтом 1/ Тп.
Спектр 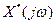 суттєво відрізняється від спектра
суттєво відрізняється від спектра 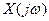 : він містить як основну складову (k=0), яка співпадає з
: він містить як основну складову (k=0), яка співпадає з 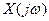 , так і додаткові складові (k=
, так і додаткові складові (k=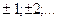 ), які виникають при квантуванні.
), які виникають при квантуванні.
Якщо ширина спектра квантуємого сигналу 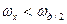 , то додаткові складові в основному діапазоні частот (
, то додаткові складові в основному діапазоні частот (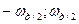 ) не спотворюють форму спектра
) не спотворюють форму спектра 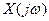 (рис.3.8,б), тобто:
(рис.3.8,б), тобто:
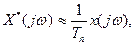 (3.29)
(3.29)
але їх наявність необхідно враховувати при відновленні неперервного сигналу за його дискретними значеннями.
При частоті квантування недостатньо високій (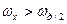 ) в основному діапазоні спектр
) в основному діапазоні спектр 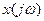 спотворюється прилеглими складовими з
спотворюється прилеглими складовими з 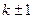 (рис.3.8,в).
(рис.3.8,в).
На рис.3.8,г показана амплітудно-частотна характеристика фільтра (формуючого елемента) для відновлення в неперервній формі квантованого сигналу при 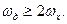 Штриховою лінією показана АЧХ ідеального фільтра низької частоти:
Штриховою лінією показана АЧХ ідеального фільтра низької частоти:
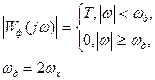 (3.30)
(3.30)
Реальний фільтр (суцільна лінія) має АЧХ:
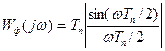 (3.31)
(3.31)
Цей фільтр дещо спотворює спектр 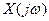 та частково пропускає гармоніки бокових складових з
та частково пропускає гармоніки бокових складових з 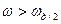 .
.
Дата добавления: 2014-01-06; Просмотров: 468; Нарушение авторских прав?; Мы поможем в написании вашей работы!