Функциональные ряды

Вопросы.

Функциональные ряды

Лекция 11

1. Определение функционального ряда.

2.Дайте определение степенного ряда.

3.Сформулируйте теорему Абеля.

4.Что называется радиусом сходимости степенного ряда?

5.Как определить интервал сходимости степенного ряда?

6.Какие способы определения радиуса сходимости степенного ряда вы знаете?

Функциональным называется ряд вида

(1)

При конкретном значении ряд (1) становится числовым рядом. Следовательно при одних значениях ряд (1) может сходится, при других – расходится. Множество значений , при которых ряд (1) сходится, называется областью сходимости ряда (1). Так как в области сходимости ряда его сумма является некоторой функцией от , то сумму ряда будем обозначать .

Пример 1. Очевидно, что при 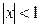ряд

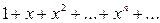
Является убывающей геометрической прогрессией () с суммой 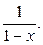Следовательно в (-1,1) ряд сходится и

Пусть

- остаток ряда. Тогда в области сходимости ряда (10)

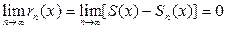
Дата добавления: 2014-01-06