
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема сложения вероятностей. Вероятность появления хотя бы одного из событий равна
|
|
|
|
Вероятность появления хотя бы одного из событий  равна
равна

Следствие 2. Если события  попарно несовместные, то
попарно несовместные, то

Действительно в этом случае 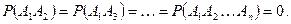
Пример 4. Производится три выстрела по одной мишени. Вероятность попадания при первом выстреле -  , при втором -
, при втором -  , при третьем -
, при третьем -  . Найти вероятность хотя бы одного попадания.
. Найти вероятность хотя бы одного попадания. 
Решение. Пусть  - попадание при первом выстреле,
- попадание при первом выстреле, 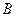 - при втором,
- при втором,  - при третьем,
- при третьем, 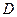 - хотя бы одно попадании при трех встрелах. Тогда
- хотя бы одно попадании при трех встрелах. Тогда  , где
, где 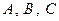 - совместные независимые в совокупности. Тогда
- совместные независимые в совокупности. Тогда
 Следствие 3. Если попарно несовместные события
Следствие 3. Если попарно несовместные события  образуют полную группу, то
образуют полную группу, то
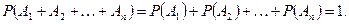
Следствие 4. Для противоположных событий

Иногда при решении задач легче найти вероятность противоположного события. Например в примере 4 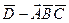 - промах при трех выстрелах. Так как
- промах при трех выстрелах. Так как 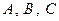 независимые в совокупности, и
независимые в совокупности, и  то
то
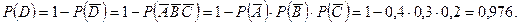
Следствие 5. Вероятность появления хотя бы одного из событий  , независимых в совокупности равна
, независимых в совокупности равна
 (1)
(1)
где 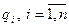 - вероятности появления событий
- вероятности появления событий  .
.
В случае, если  имеют одинаковую вероятность
имеют одинаковую вероятность  , то формула (1) имеет вид
, то формула (1) имеет вид  , где
, где 
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 330; Нарушение авторских прав?; Мы поможем в написании вашей работы!