
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неоднородные уравнения
|
|
|
|
Для уравнения с постоянными коэффициентами и специальными правыми частями 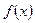 частные решения можно найти проще, не применяя метод вариации.
частные решения можно найти проще, не применяя метод вариации.
Пусть 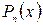 и
и 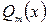 - многочлены
- многочлены 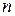 -ой и
-ой и 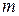 -ой степени, а
-ой степени, а 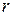 - кратность корня
- кратность корня 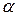
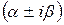 характеристического уравнения, причем, если
характеристического уравнения, причем, если 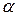
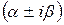 не является корнем, то
не является корнем, то 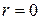 .
.
Если
1.  , то частное решение ищут в виде
, то частное решение ищут в виде 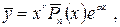 где
где 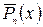 - много-член с неопределенными коэффициентами.
- много-член с неопределенными коэффициентами.
2. 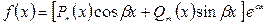 , то
, то 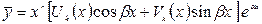 , где
, где 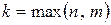 , а
, а 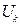 и
и 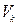 - многочлены с неопределенными коэффициентами.
- многочлены с неопределенными коэффициентами.
Пример 3. Найти общее решение уравнений
а) 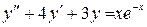 (8)
(8)
1) Найдем общее решение однородного уравнения 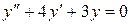 .
.
2) 
3) Найдем частное решение уравнения (8): 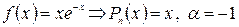 - однократный корень
- однократный корень 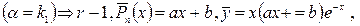 где
где 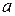 и
и 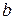 надо подобрать так, чтобы
надо подобрать так, чтобы 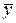 был решением (8).
был решением (8). 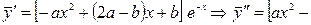
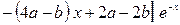 .
.
Подставляя 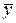 ,
, 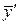 ,
, 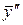 в (8) и приравнивая коэффициенты у одинаковых степеней
в (8) и приравнивая коэффициенты у одинаковых степеней 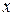 , получим
, получим
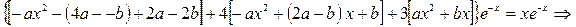

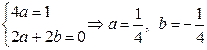 .
.
Частное решение 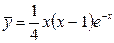 , а общее -
, а общее -  .
.
б) 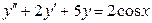 .
.
1) 
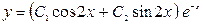 - общее решение однородного уравнения.
- общее решение однородного уравнения.
2) 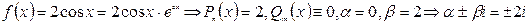 не корнем
не корнем
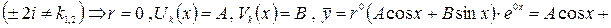
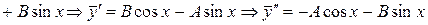 . Подставляя
. Подставляя 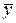 ,
, 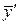 ,
, 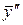 в уравнение, получим.
в уравнение, получим.

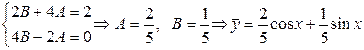 .
.
Общее решение
 .
.
Пример из экономики. Модель Самуэльсона – Хикса.
Решение уравнений, вида
 ,
,
где 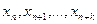 - члены некоторой числовой последовательности,
- члены некоторой числовой последовательности, 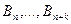 - постоянные числа,
- постоянные числа, 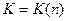 - некоторая функция натурального числа, называется линейным разностным уравнением
- некоторая функция натурального числа, называется линейным разностным уравнением 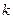 -ого порядка.
-ого порядка.
Методы решения данного уравнения, широко используемого в экономике, аналогичны решению ЛДУ с постоянными коэффициентами.
Продемонстрируем это для разностных уравнений 2-ого порядка, вида:
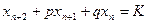 .
.
Так же как и для ЛДУ, общее решение данного уравнения определяется по формуле:
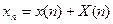 ,
,
где 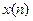 - некоторое частное решение данного уравнения, а
- некоторое частное решение данного уравнения, а  - общее решение соответствующего однородного уравнения. Для нахождения последнего решения необходимо найти корни характеристического уравнения
- общее решение соответствующего однородного уравнения. Для нахождения последнего решения необходимо найти корни характеристического уравнения 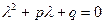 .
.
Могут возникнуть три варианта.
1. Оба корня действительные и различные, тогда 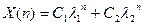 .
.
2. Оба корня действительные и равные 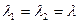 , тогда
, тогда  .
.
3. Корни комплексно-сопряженные, тригонометрическая форма, вида 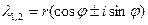 , тогда
, тогда 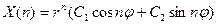 .
.
Пример 4. Решить уравнение
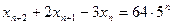 .
.
Решение. Методом неопределенных коэффициентов найдем частное решение в виде: 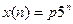 . Подставляя это выражение в уравнение, получим
. Подставляя это выражение в уравнение, получим
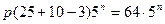 .
.
Следовательно, 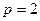 и
и 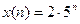 .
.
Решая характеристическое уравнение: 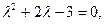 находим
находим 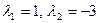 . Таким образом, общее решение уравнения имеет вид:
. Таким образом, общее решение уравнения имеет вид:
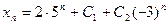 .
.
Рассмотрим уравнение Хикса:
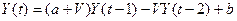 .
.
Частное решение данного уравнения найдем из условия
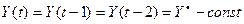 ,
,
Это так называемое равновесное решение. Подставляя его в данное уравнение, получаем  , откуда получаем
, откуда получаем 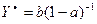 . Заметим, что множитель
. Заметим, что множитель 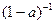
 называется мультипликатором Кейнса и является одномерным аналогом матрицы полных затрат.
называется мультипликатором Кейнса и является одномерным аналогом матрицы полных затрат.
В этих терминах рассмотрим модель Самуэльсона – Хикса при условии:  В этом случае уравнение примет вид:
В этом случае уравнение примет вид:
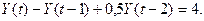
Его частным решением будет функция 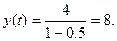 найдем корни характеристического уравнения
найдем корни характеристического уравнения  Имеем
Имеем 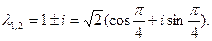
Таким образом, общим решением искомого уравнения будет
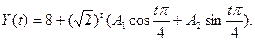
В зависимости от 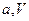 возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.
возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.
Литература
- Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. М.: Наука, 1985г.
- Краснов М.Л. Обыкновенные дифференциальные уравнения. М.: Высшая школа 1983г.
- Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.: Наука, 1985г.
- Сборник индивидуальных заданий по высшей математике ч.1-3 Под редакцией Рябушко А.П. Минск.: Вышейшая школа, 2001 г.
- Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Ч.1,2 М.: Высшая школа,1986 г.
- Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). М.: Высшая школа, 1983 г.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!