С положительными членами

Достаточные признаки сходимости для рядов

Теорема 2. (Первый признак сравнения).Пусть имеется два ряда

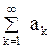(10.1)

и

(10.2)

с положительными членами 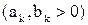, удовлетворяющими неравенству

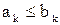(10.5)

для всех, за исключением, быть может, конечного числа членов рядов.

Тогда если ряд (10.2) сходится, то ряд (10.1) также сходится, если же ряд (10.1) расходится, то ряд (10.2) также расходится.

Пример4. Исследуем сходимость ряда

.

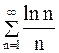Для сравнения используем расходящийся гармонический ряд

.

Пр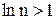и и ,

поэтому, согласно первому признаку сравнения, исследуемый ряд расходится.

Для сравнения обычно используют такие известные ряды как геометрическая прогрессия или ряд Дирихле.

Рядом Дирихленазывается числовой ряд вида

.

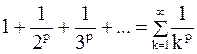Немного позже мы докажем, что ряд Дирихле при 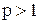сходится, а при расходится. При 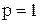от превращается в гармонический ряд.

Пример5. Исследуем сходимость ряда

.

Для сравнения возьмем сходящийся ряд Дирихле

.

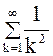(Здесь 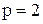). Поскольку 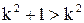, то 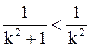для всех .

И исследуемый ряд сходится.

Теорема 3. (Предельный признак сравнения).

Пусть ряды

(10.1)

и

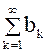(10.2)

с положительными членами таковы, что существует конечный ненулевой предел

.

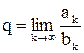
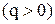Тогда ряды (10.1) и (10.2) сходятся или расходятся одновременно.

Пример. Исследуем сходимость ряда

.

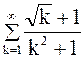Для сравнения подберем ряд Дирихле следующим образом. Оставив в числителе и знаменателе слагаемые с наибольшей степенью, получим ряд с членами

,

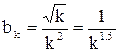которые составляют сходящийся ряд Дирихле с параметром .

Найдем число .

Итак, согласно предельному признаку, исследуемый ряд сходится.

Теорема 4. (Признак Даламбера)

Пусть у ряда

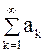
где 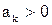существует предел отношений

, (10.6)

тогда:

а) если , то этот ряд сходится,

в) если или этот ряд расходится.

При данный признак не применим.

Пример7. Исследуем сходимость ряда .

Для этого ряда , поэтому

,

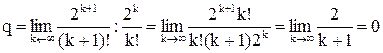т.к. , то исследуемый ряд сходится.

Теорема 5. (Радикальный признак Коши).Пусть в ряде ,

где , существует предел

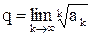. (10.7)

Тогда:

а) если , то этот ряд сходится,

в) если или ,то этот ряд расходится.

При , как и в предыдущем случае, признак Коши не применим.

Пример8. Исследуем сходимость ряда

.

Вычислим требуемый предел.

. (Второй замечательный предел). Поскольку , то исходный ряд сходится.

Теорема 6. (Интегральный признак Коши).

Пусть имеется ряд

(10.1)

и несобственный интеграл

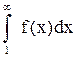, (10.9)

такие, что выполняются следующие условия:

а) для целых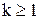

,

б) функция 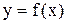непрерывна, неотрицательна и не возрастает на промежутке .

Тогда ряд (10.1) и интеграл (10.9) сходятся или расходятся одновременно.

Доказательство можно продемонстрировать на рисунке 10.

Рис. 10

Пример 9. Исследуем сходимость ряда Дирихле для различных :

.

Функция получается путем замены индекса суммирования на . При 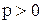она удовлетворяет всем условиям теоремы. Она непрерывна, в промежутке , т.к. имеет разрыв только в точке 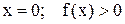в этом промежутке и убывает в нем, т.к. ее знаменатель возрастает с ростом .

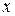Пусть, тогда

,

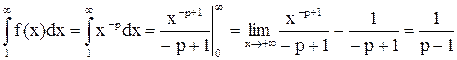т.е. при 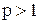этот интеграл и ряд Дирихле сходятся.

При этот интеграл и ряд Дирихле расходятся.

При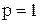

.

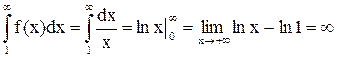Заметим, что при члены ряда Дирихле не стремятся к нулю, поэтому он расходится согласно следствию из необходимого признака.

Следствие. Интегральный признак можно применять и к рядам вида

.

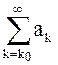В этом случае условия, накладываемые на функцию 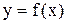должны выполняться на промежутке .

Интегральный признак следует применять в тех случаях, когда возможно интегрирование функции .

Пример10. Исследуем сходимость ряда

.

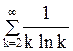Понятно, что член 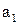этого ряда по написанной формуле определить не- возможно.

Элементарная функция 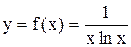определена в промежутке 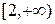, поэтому она непрерывна в промежутке , положительна в нем и убывает, т.к. ее знаменатель возрастает с ростом .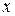

Найдем несобственный интеграл

.

Т.е. исследуемый ряд расходится.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М.:Наука, 1988г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.:Наука, 1985г.

3. Кудрявцев Л.Д. Курс математического анализа. Т. 1,2, М.: Высшая школа, 1981г.

4. Бронштейн И.Н.,Семендяев К.А. Справочник по математике для инженеров.М.: Высшая школа,1997.

5. ИДЗ. Дифференциальное исчисление функции одной переменной. Под редакцией Рябушко А.П., ч.1,2 Минск, «ВШ», 2002г.

Дата добавления: 2014-01-06