Числовые характеристики случайной величины

Числовые характеристики выражают наиболее существенные особенности данного распределения.

Определение. Математическим ожиданием случайной величины Х называется

а) Х – дискретная величина

б) Х – непрерывная величина

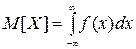
Математическое ожидание можно рассматривать как центр рассеивания величины Х. Если проводится опытов, то 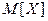приближенно равна среднему арифметическому наблюдаемых значений Х.

Основными характеристиками рассеивания Х около 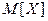являются и среднее квадратическое отклонени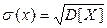е , где :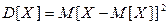

а) Х – дискретная

Кроме указанных числовых характеристик используются и другие: мода, медиана, моменты и др.

Начальные и центральные теоретические моменты.

Определение. Начальным моментом порядка к случайной величины Х называют маматическое ожидание величины Х^к:

Аналогично для дисперсии

Определение. Центральным моментом порядка к сл.вел. Х называют математическое ожидание и величины :

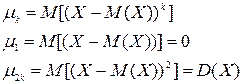
Легко выводятся связь между и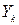

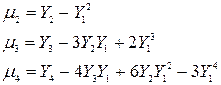
Пример 2. Дано

X	0,1
p	0,4	0,2	0,15	0,25

Экономический пример 3. Компания продает некоторый продукт, учет продаж которого ведется в тысячах штук. Закон распределения объема ежемесячных продаж продукта представлен в таблице. Найдем ожидаемое среднее значение числа месячных продаж.

Число единиц товара х, тыс, шт.	Р(х)
	0,2 0,3 0,2 0,2 0,1
	1,0

Решение. Из формулы (3.4) следует, что М (Х) = 5000∙0,2 + 6000∙0,3+ + 7000∙ 0,2 + 8000∙ 0,2 + 9000∙ 0,1 = 1000 + 1800 + 1400 +
+ 1600 + 900 = 6700.

Пример 4. Каждый день местная газета получает заказы на новые рекламные объявления, которые будут напечатаны в завтрашнем номере. Число рекламных объявлений в газете зависит от многих факторов: дня недели, сезона, общего состояния экономики, активности местного бизнеса и т. д. Пусть X – число новых рекламных объявлений, напечатанных в местной газете в определенный день. X – случайная величина, которая может быть только целым числом. В нашем примере случайная величина X принимает значения 0; 1; 2; 3; 4; 5 с вероятностями 0,1; 0,2; 0,3; 0,2; 0,1; 0,1 соответственно. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X – числа рекламных объявлений в газете в заданный день.

Решение. Ряд распределения случайной величины X

xi
P (xi) = pi	0,1	0,2	0,3	0,2	0,1	0,1

Вычисление математического ожидания числа рекламных объявлений:

хi							n
P (хi)	0,1	0,2	0,3	0,2	0,1	0,1
хiP (хi)	0,0	0,2	0,6	0,6	0,4	0,5	М (Х) = 2,3

Можно сказать, что в среднем 2,3 рекламных объявления ежедневно помещаются в газете. Это – ожидаемое среднее число рекламных объявлений в заданный день. Дисперсия вычисляется так:

σ² = 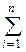[ x_i–M (X)]² P (x_i) = (0–2,3)² + (1–2,3)² + (2–2,3)² + (3–2,3)² + (4–2,3)² + (5 – 2,3)² = 2,01. Среднеквадратическое отклонение

Дата добавления: 2014-01-06