Производная по направлению и градиент функции нескольких переменных

Рассмотрим скорость изменения функции трех переменных при перемещении из точки 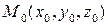в направлении единичного вектора 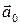, определяемого своими координатами – направляющими косинусами: . Для этого рассмотрим прямую , проходящую через точку 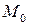с направляющим вектором 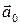. Ее параметрические уравнения имеют вид

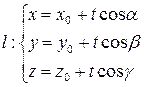(1)

Заметим, что поскольку вектор 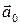единичный, то измерение параметра 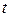на величину 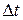означает перемещение вдоль этой прямой на отрезок длины 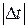и, что при 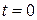точка на прямой соответствует .

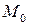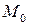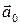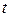Определение. Производной функции в точке по направлению вектора называется производная ограничения этой функции на прямую по при 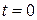(рис.).

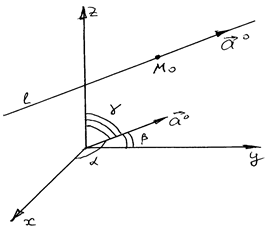
Обозначается эта производная .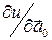

Получим формулу для вычисления производной по направлению вектора 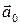. Для этого подставим из (1) в , получим

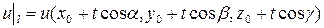, поэтому

. (2)

Определение. Вектор с координатами – частными производными функции 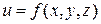называется градиентом функции, он обозначается так:

.

Из (2) получим другую формулу, выражающую через градиент :

(3)

Для произвольного вектора 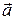, учитывая, что ,

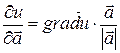. (4)

Если 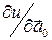требуется вычислить в некоторой точке 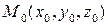, то в (3) и (4) необходимо также вычислять в этой точке.

Пример. Найти скорость изменения температуры тела, заданной функцией 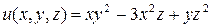в точке в направлении вектора 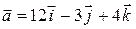. Для этого найдем частные производные и градиент поля :

; ; ;

;

.

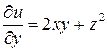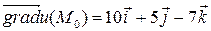Далее, 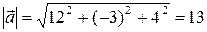, поэтому из (2) имеем

.

Из вида уравнения касательной плоскости и формулы вектора-градиента можно сделать вывод, что градиент является нормальным вектором к этой плоскости.

Пример из экономики. Вектор, составленный из частных производных функции полезности называется вектором предельных полезностей или градиентом. Он показывает направление наибольшего роста значений функции. Немецкий экономист К.Госсен сформулировал основополагающее свойство функции полезности: с увеличением потребления товара его полезность уменьшается. То есть если вы голодны, то первый гамбургер съедите с большой охотой, второй уже не с таким аппетитом, и т.д. На математическом языке это означает, что предельные полезности убывают с возрастанием аргументов - количества потребляемых товаров, т.е. вторые частные производные должны быть отрицательные.

Дата добавления: 2014-01-06