
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная высших порядков
|
|
|
|
Определение. Частной производной  –го порядка функции
–го порядка функции 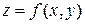 называется частная производная от одной из ее производных
называется частная производная от одной из ее производных 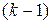 порядка.
порядка.
Это рекуррентное определение дает возможность получить  –ую частную производную функцию путем нахождения последовательно
–ую частную производную функцию путем нахождения последовательно  частных производных от этой функция. Сама функция
частных производных от этой функция. Сама функция  считается производной нулевого порядка.
считается производной нулевого порядка.
Как мы установили ранее, производных первого порядка у функции  две
две 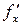 и
и  . Взяв от этих производных производные по
. Взяв от этих производных производные по 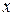 и
и  , получим четыре производных второго порядка:
, получим четыре производных второго порядка:
 ,
,  ,
,  ,
,  .
.
Взяв от этих производных производные по 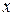 и
и  , получим восемь частных производных третьего порядка и так далее. Производных
, получим восемь частных производных третьего порядка и так далее. Производных  –го порядка у функции двух переменных имеется
–го порядка у функции двух переменных имеется 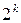 .
.
Пример. Найдем все частные производные первого и второго порядков у функции
 .
.
 ,
,  ,
,  ,
,
 ,
, 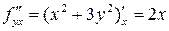 ,
,  .
.
В этом примере 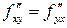 и это не случайно.
и это не случайно.
Определение. Частная производная функции, в которой присутствуют дифференцирования по разным переменным, называется смешанной производной.
Смешанными производными второго порядка у функции двух переменных являются  и
и  .
.
Теорема о смешанных производных.
Пусть функция 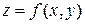 и ее производные
и ее производные 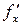 ,
,  ,
,  ,
,  непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки  . Тогда в этой точке ее смешанные производные второго порядка равны между собой:
. Тогда в этой точке ее смешанные производные второго порядка равны между собой:
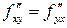 .
.
Следствие. Пусть все частные производные функции
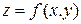
до 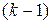 –го порядка включительно и все ее смешанные производные
–го порядка включительно и все ее смешанные производные  –го порядка непрерывны в некоторой окрестности т.
–го порядка непрерывны в некоторой окрестности т.  . Тогда в этой точке ее смешанные производные
. Тогда в этой точке ее смешанные производные  –го порядка отличающиеся только очередностью дифференцирования совпадают.
–го порядка отличающиеся только очередностью дифференцирования совпадают.
Без доказательства.
Это следствие обосновывает следующее обозначение смешанной производной  –го порядка, в которой встречается
–го порядка, в которой встречается 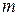 дифференцирований по
дифференцирований по 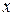 и
и  по
по  :
:
 .
.
При выполнении условий следствия, порядок в котором производятся эти дифференцирования, не влияет на результат.
Пример. Пусть  . Найдем
. Найдем 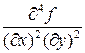 .
.

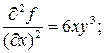

 .
.
При любом другом порядке дифференцирования, в котором будут по два дифференцирования по 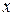 и по
и по  результат получится тем же.
результат получится тем же.
Определение. Функция 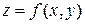 , имеющая все непрерывные частные производные до
, имеющая все непрерывные частные производные до  –го порядка включительно в окрестности точки
–го порядка включительно в окрестности точки  , называется
, называется  раз дифференцируемой в этой точке.
раз дифференцируемой в этой точке.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 528; Нарушение авторских прав?; Мы поможем в написании вашей работы!