Экстремум функции нескольких переменных

Определение. Точка называется точкой максимума функции 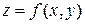, если у этой точки имеется окрестность 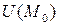такая, что для всех из этой окрестности выполняется неравенство

.

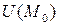Если для всех из окрестности выполняется неравенство

,

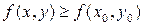то точка 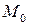называется точкой минимума.

Значение функции в точке максимума 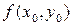, называется максимумом функции, а ее значение в точке минимума – минимумом.

Точки максимума и минимума называются экстремальными точками функции, а максимумы и минимумы называются экстремумами функции.

Пусть функция 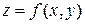определена в некоторой окрестности точки 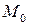. Если в 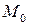каждая частная производная 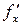и равна нулю или не существует, то 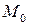называется критической точкой функции .

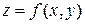Следующая теорема является аналогом необходимого условия экстремума функции одной переменной.

Теорема 1 (необходимое условие экстремума)

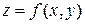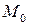Если является экстремальной точкой функции , то – критическая точка этой функции.

Доказательство. Рассмотрим функцию одного переменного 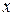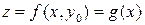. Из определения экстремальной точки следует, что точка 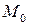– экстремальная для функции 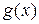. Согласно необходимому условию экстремума для функции одной переменной, 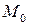критическая точка этой 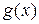, т.е.

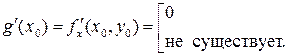
Рассмотрев функцию ,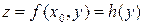

получим, что

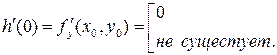
Пример. Точка является точкой минимума функции т.к. 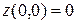, а для всех остальных точек .

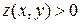Поскольку 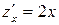и , то решение системы

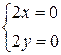
определяет критическую точку .

Пример. Точка не является экстремальной точкой функции 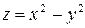, т.к. в любой ее окрестности функция принимает как значения больше 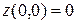при , так и значения меньше при 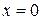. Тем не менее, поскольку 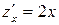, , 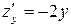координаты удовлетворяют системе

,

то точка критическая точка.

Этот пример показывает, что критическая точка может не быть экстремальной.

График функции 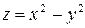является гиперболическим параболоидом, имеющим форму седла, точка называется его седловой точкой.

Дата добавления: 2014-01-06