Теорема 2. (Достаточные условия экстремума.)

Пусть функция 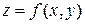трижды дифференцируема в некоторой окрестности своей критической точки .

Обозначим , , , .

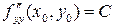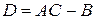Тогда:

1) Если , то точка 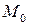экстремальная для функции 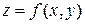, причем если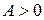 , то это точка минимума, а если , то точка 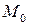, точка максимума.

2) Если , то в точке экстремума нет.

Заметим дополнительно, что при 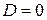для определения экстремума требуется дополнительное исследование.

Без доказательства.

Пример. Найдем экстремальные точки и экстремумы функции

.

Поскольку 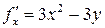и существуют для всех то, для определения критических точек необходимо решить систему уравнений

.

Отсюда получаем два решения:

и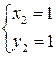

и две критические точк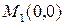и и 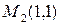. Найдем вторые частные производные функции и исследуем каждую из этих точек помощью достаточного условия экстремума.

, , .

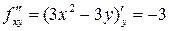а) 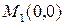. В этом случае

; ; ; .

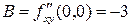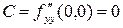Поэтому в точке 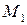экстремума нет.

б) 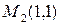. В этом случае

; ; ;

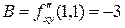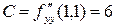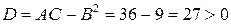
поэтому экстремальная точка. Поскольку , то это точка минимума. Значение функции в равно 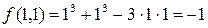, что составляет минимум функции.

Примеры из экономики. Задачи оптимизации в экономике.

Пусть z – количество продукции, выпущенной некоторой фирмой; 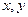- затраты ресурсов двух видов; - дифференцируемая функция. Пусть величины - заданы в натуральных единицах, 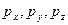- соответствующие этим единицам постоянные цены.

Тогда выручка (валовой доход) будет , а функция прибыли запишется в виде:

.

Исследуем данную функцию на экстремум. Согласно необходимому признаку локального экстремума, вычисляем:

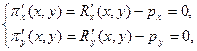
Отсюда

Согласно достаточному условию локального экстремума в критической точке должны выполняться условия: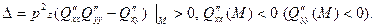

Пусть 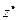- оптимальный выпуск продукции с точки зрения прибыли; 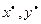- соответствующие затраты ресурсов. Если точка 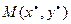является внутренней точкой области определения функции 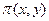, то 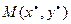- точка ее локального максимума.

Вывод: в точке локального максимума прибыли предельная выручка от каждого ресурса совпадает с его ценой.

Этот вывод сохраняется и в более общем случае, когда цена зависит от объема выручки, поскольку частные производные функции 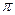имеют прежний вид.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление,

М.:Наука, 1988г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2

М.:Наука, 1985г.

3. Кудрявцев Л.Д. Курс математического анализа. Т. 1,2, М.: Высшая школа, 1981г.

4. Бронштейн И.Н.,Семендяев К.А. Справочник по математике для инженеров.

М.: Высшая школа,1997.

5. ИДЗ. Дифференциальное исчисление функции одной переменной. Под редакцией

Рябушко А.П., ч.1,2 Минск, «ВШ», 2002г.

Дата добавления: 2014-01-06