Основні визначення. Струминна модель потоку.

Рідину, що рухається, можна розглядати як сукупний рух матеріальних точок по відповідних траєкторіях. Траєкторія - слід частки, що рухається. Для кожного моменту часу графічно можна представити положення частки і її швидкість у вигляді вектора певної довжини і напряму. Сукупність усіх векторів швидкості матеріальних точок буде називатись полем швидкостей або векторним полем.

Сполучивши лінією всі подальші за часом положення матеріальної точки, одержимо лінію, яку називають лінією течії. Лінія течії задовольняє вимозі, згідно з якою у кожній точці вектор швидкості співпадає з дотичною до лінії течії (рис.6.1). При сталому русі лінія течії співпадає з траєкторією частки, що рухається.

Якщо u_x, u_y, u_z не рівні нулю, то рух називають просторовим, якщо одна з компонент рівна нулю, то одержуємо плоский рух, якщо дві компоненти рівні нулю, то одержуємо одновимірний рух.

Якщо за час dt частка рідини пройде за напрямком лінії течії шлях dl з компонентами на координатних осях, рівними dx, dy, dz, то складові цієї швидкості становитимуть

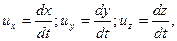
а тому

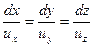. (6.1)

Система рівнянь (6.1) є рівнянням лінії течії. Для плоского руху, відповідно можна записати

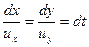
або

(6.2)

Рівняння (6.2) є рівнянням лінії течії плоского потоку.

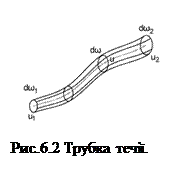
Струминна модель потоку введена Л.Ейлером. Основу цієї моделі складає поняття про елементарну струминку. Проведемо через кожну точку нескінченно малого контуру площею dω (рис. 6.2.) лінії течії. В результаті отримаємо поверхню, яку називають трубкою течії. Поверхня трубки течії непроникна для рідини. Це випливає з визначення для лінії течії. Обмежену трубкою течії рідину називають елементарною струминкою. Поверхню нормальну в кожній точці до лінії течії називають живим перетином струминки. У загальному випадку поверхня живого перетину є криволінійною, перетворюючись у плоску при паралельно-струминному потоці. При вивченні багатьох гідравлічних явищ трапляються випадки, коли струминки не паралельні одна одній, але кривина струминок невелика і кут розходження між ними дуже малий. Такий рух називають плавно-змінним.

З непроникності трубки течії випливає, що кількість рідини, що протікає через живий перетин в одиницю часу є величина постійна, тобто

u₁dω₁ = u₂dω₂= u₃dω₃ ... = u_ndω_n = dQ (6.3)

Величину dQ називають витратою елементарної струминки, тобто, це - кількість рідини, що протікає через живий перетин елементарної струминки за одиницю часу. Розрізняють об’ємну витрату (див.(6.3)), масову m (кг/c) і вагову G (Н/с), які для елементарної струминки запишуться як

dm=rudω та dG=rgudω

Якщо живий перетин кінцевий, то у загальному випадку розподіл швидкості по живому перетину нерівномірний, тому витрата визначається як інтеграл

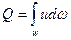(6.4)

або

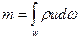(6.5)

Вагова витрата, відповідно G=mg.

Течію з кінцевим живим перетином називають потоком. Рівняння (6.4) та (6.5) часто називають рівняннями витрат.

Для врахування умов руху рідини залежно від форми і розмірів живого перерізу в гідравліці використовують поняття змоченого периметра і гідравлічного радіуса.

Змоченим периметром c називають ту частину периметра живого перерізу, по якій рідина стикається зі стінками, що її обмежують.

Гідравлічним радіусом R називають відношення площі живого перерізу до змоченого периметра, тобто

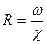(6.6)

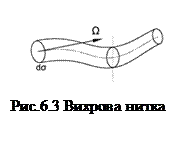
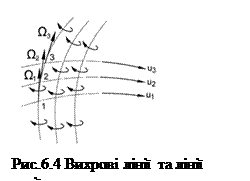Окрім поступального руху рідина може здійснювати обертальний рух та рух деформації (див. далі теорему Коші-Гельмгольца). Потік рідини, що здійснює обертальний рух називають вихровим. Вихровий рух характеризується кутовою швидкістю обертання елементарної рідкої частки. Представивши кутову швидкість частки вектором (за правилом правого свердлика) можна графічно представити усі подальші у часі положення осі обертання частки. Лінію, у кожній точці якої вектор вихору збігається за напрямом з дотичною до неї, називають вихровою лінією. Вихрові лінії, проведені через кожну точку нескінченно малого контуру (рис. 6.3.) утворюють вихрову нитку. При контурі кінцевого розміру одержуємо вихровий шнур.

Очевидно, що за аналогією з (6.1) диференціальні рівняння вихрової лінії можуть бути встановлені як наслідок визначення цієї лінії. Рівняння вихрової лінії мають вигляд

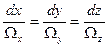, (6.7)

де W _x=2ω_x, W _y=2ω_y, W _z=2ω_z – компоненти вихору швидкості, що рівні подвоєним за значенням компонентам вектору кутової швидкості.

Вихрові лінії і лінії течії взагалі не суміщаються (рис.6.4).

Одиниці вимірювання та розмірності швидкостей, прискорень і витрат наведені у таблиці 6.1.

Таблиця 6. 1

Фізична величина	Позначення	Одиниці вимірювання	Розмірність
СІ	СГС	МКГСС	СІ, CГС	МКГСС
Швидкість	ux, uy, uz	м/с	см/с	м/с	LT^--1	LT^--1
Прискорення	ax, ay, az	м/c^2	cм/c^2	м/c^2	LT^--2	LT^--2
Кутова швидкість	ωx, ωy, ωz	рад/с	рад/с		T^--1	T^--1
Витрата об'ємна	q, Q	м^3/c	cм^3/c	м^3/c	L^3T^—1	L^3T^--1
Витрата масова	m, M	кг/с	г/c	-	MT^-1	-
Витрата вагова	G	H/c	кгс/c		MLT^-3 GT^-1

Дата добавления: 2014-01-07