Характеристики дінамічних рядів

Для оцінки швидкості та інтенсивності розвитку різних соціальних явищ статистика використовує наступні взаємозв”язані характеристики:

1) абсолютний приріст;

2) темпи зростання;

3) відносний приріст;

4) абсолютне значення 1% приросту.

Вони обчислюються шляхом зіставлення рівнів ряду. Рівень, з яким проводять порівняння, називається базою. База може бути постійна, коли використовують для порівняння початковий рівень у ₀, або змінна, коли для зіставлення використовують попередній рівень у _t-1.

Обчислені з допомогою постійної бази характеристики динаміки називають базисними, а з допомогою змінної бази (зіставлення суміжних рівнів) – ланцюговими.

Абсолютний приріст відображає абсолютну швидкість змінювання рівнів ряду за певний інтервал часу. Обчислюється як різниця рівнів ряду. Знак (+, -) показує напрям динаміки. Ланцюгові і базисні прирости адитивно зв язані: сума ланцюгових приростів дорівнює загальному приросту за весь період.

.

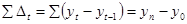Абсолютний приріст залежно від статистичної природи показника може бути відносною величиною.

Приклад: частка використаного національного доходу у 2000 році становила 82%, а в 2005 році - 79%, тобто зменшилась на 3% ( = 79 - 82 = - 3%).

Теми зростання К _t - це відносна величина, що характеризує інтенсивність зміни рівнів ряду. Являє собою кратне відношення рівнів, визначається у коефіціентах чи відсотках. Ланцюгові

і базисні

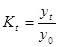
темпи зростання мультипликативно зв”язані. Добуток ланцюгових темпів динаміки дорівнює кінцевому базисному .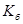

К₁*К₂*......*К_n = ,

де 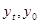- кінцевий та перший рівні динамічного ряду

Співвідношення абсолютного приросту і базового рівня є вимірником відносної швидкості зростання. Нескладні алгебраїчні перетворення цього відношення дають відхілення темпу зростання К_t від бази порівняння, яка становить 100%. Відносну швидкість зростання називають темпом приросту Т_t, який на відміну від темпу зростання завжди виражають у відсотках.

.

Ланцюгові темпи приросту не мають властивостей адитивності чи мультипликативності. З базисними темпами приросту вони співвідносяться через темп зростання.

Абсолютне значення 1% приросту 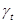- це частка від ділення абсолютного приросту на темп його (приросту).

.

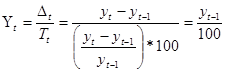Розрахунок має економічний зміст тільки на ланцюговій основі. Таким чином, вага відсотка приросту залежить від базисного рівня.

Для узагальнення оцінок швидкості і інтенсивності використовують середні величини.

Середній абсолютний приріст 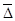обчислюють за формулою середньої арифметичної простої із ланцюгових приростів, тобто (на основі адитивності зв язку)

,

де n - кількість років періоду.

Середній темп зростання 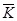розраховують за формулою середньої геометричної (на основі мультипликативного зв”язку між ланцюговими і базисними темпами зростання).

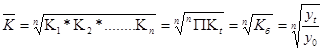
де n – кількість проміжків часу, що входять у часовий період;

- кінцевий базисний темп зростання;

- початковий та кінцевий рівні ряду динаміки.

Абсолютне прискорення зростання або уповільнення визначають зіставленням однойменних характеристик швидкості. Якщо інтервали часу однакові, зіставляють базисні характеристики швидкості, якщо неоднакові – користуються середніми швидкостями

.

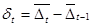Якщо > 0, то це абсолютне прискорення зростання, якщо < 0 – абсолютне уповільнення зростання.

Темп уповільнення (зростання) динаміки 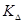визначають зіставляючи абсолютні середньорічні прирости.

.

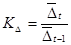Коефіцієнт уповільнення (зростання) відносної швидкості розвитку φ_t визначається за формулою

φ_t =

10.3. Аналіз структурних зрушень.

Структура будь якої статистичної сукупності динамічна. Зміна часток окремих складових частин сукупності – це наслідок структурних зрушень.

Структурні зрушення оцінюють за допомогою абсолютних і відносних характеристик дінаміки:

- абсолютного приросту j- частки в процентних пунктах

;

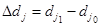- темпу зростання j -частки

.

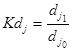Сума абсолютних приростів часток дорівнює нулю, а загальний темп зростання – одиниці.

Характеристики структурних зрушень взаємозв’язані.

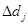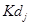= (-1).

Очевидно, що для складових частин, де темп зростання Кd>1, абсолютний приріст Δd додатний і, навпаки, при Кd<1 – від’ємний.

Абсолютні прирости і темпи зростання часто непропорційні одне одному.

Як узагальнюючі характеристики інтенсивності структурних зрушень застосовують – лінійний і 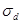- квадратичний коефіцієнти. Їх обчислюють на основі абсолютних приростів часток 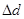, тобто

.

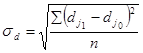Знаючи темпи зростання часток, обчислюють квадратичний коефіцієнт , який чутливіше реагує на зміни структури.

Темп зростання адитивного показника у = Σу_і можна виразити через темпи зростання його складових частин у формі середньої арифметичної зваженої:

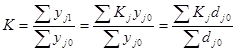
Такий самий зв’язок існує між темпами приросту цілого і складових частин. Якщо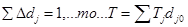

10.4. Особливості вимірювання взаємозв’язків за даними динамічних рядів.

При вивченні кореляційних зв”язків у багатомірних динамічних рядах виникають складнощі, спричинені залежністю рівнів, їх автокореляцією. Наявність автокореляції порушує одну з передумов регресійного аналізу – незалежність спостережень і приводить до викривлення його результатів.

Необхідно усувати автокореляцію. Є такі способи її усунення:

- спосіб різнецевих перетворень;

- введення змінної величини в рівняння регресії У=f(х₁,х_2,t).

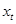Спосіб різницевих перетворень є найпростішим. Замість первинних рівнів взаємозв’язаних рядів динаміки і використовують абсолютні прирости (різниці). Різниці першого порядку ∆у = у _t –у_t -₁; ∆х =х – х_t-1 усувають лінійний тренд, а регресійне рівняння набуває вигляду.

∆ у = 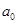+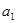∆ х

де 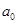- параметр, який не має економічного змісту;

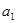- звичайний коефіцієнт регресії.

Якщо тенденція нелінійна, доцільно застосовувати спосіб відхилень від тенденції, коли замість первинних рівнів у _t і х _t використовують їх відхилення від теоретичних рівнів, обчислених за трендовими кривими.

, .

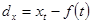У другому способі усунення автокореляції змінна величина t виконує роль фактора часу. Якщо початок відліку часу перенести в середину динамічного ряду, то Σt = 0. Вибір функції регресії залежить від зв”язку між показниками динамічного ряду.

Параметри функції визначають методом найменших квадратів, розв”язуючи систему нормальних рівнянь.

У разі усунення автокореляції залишки 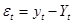мають бути незалежними. Цю гіпотезу перевіряють за допомогою коефіціента автокореляції τ, який обчислюється з певним часовим зсувом – лагом p.

При p = 1

.

Коефіцієнт автокореляції змінюється в межах -1 ≤ τ ≤1.

Об’єктивний висновок щодо наявності автокореляції передбачає перевірку її істотності за допомогою критеріїв математичної статистики. Якщо фактичне значення коефіцієнта автокореляції менше критичного, то автокореляція відсутня.

Дата добавления: 2014-01-07