
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множинна регресія
|
|
|
|
Множинна регресія дає можливість оцінити зв”язок результативної ознаки з будь якою факторною при фіксованому значенні інших, включених в регресійну модель.
На практиці часто використовують множинні, багатофакторні рівняння регресії, коли на величину результативної ознаки впливає 2, 3 і більше факторів.
І етап. Теоритичне обгрунтування моделі і вибору факторних ознак.
Слід врахувати тісноту кореляційного зв”язку між ознаками. При наявності зв”язку, близького до функціонального (мультиколінеарності), оцінки параметрів багатофакторної моделі будуть ненадійними. Для оцінки мультиколінеарності між ознаками достатньо обмежити відповідні коефіціенти кореляції (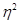 ) двох факторних ознак. Якщо він близький до 1, то одну з них треба виключити. На цьому етапі важливо не тільки вибрати фактори, а й розкрити структуру взаємозв”зку між ними.
) двох факторних ознак. Якщо він близький до 1, то одну з них треба виключити. На цьому етапі важливо не тільки вибрати фактори, а й розкрити структуру взаємозв”зку між ними.
Обгрунтування функціонального вигляду багатофакторного рівняння регресії - це складна проблема.
Аналіз парних зв”язків непридатний, тому що фактори взаємозв”язані, а визначити зв”язок між у і 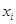 при фіксованих значеннях інших факторних ознак дуже складно. Тому на практиці найчастіше використовують багатофакторні лінійні рівняння та рівняння, що приводять до лінійних відповідними перетвореннями, тобто
при фіксованих значеннях інших факторних ознак дуже складно. Тому на практиці найчастіше використовують багатофакторні лінійні рівняння та рівняння, що приводять до лінійних відповідними перетвореннями, тобто
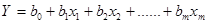 .
.
Параметр рівняння 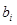 називають частинним коефіцієнтом регресії.
називають частинним коефіцієнтом регресії.
Він показує, як у середньому, змінюється у зі зміною факторної ознаки 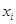 на одиницю її власного виміру за умови, що інші факторні ознаки залишаються незміними.
на одиницю її власного виміру за умови, що інші факторні ознаки залишаються незміними.
Для визначення параметрів 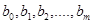 складають і розв”язують систему нормальних рівнянь.
складають і розв”язують систему нормальних рівнянь.
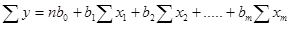
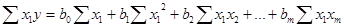
.
.
.
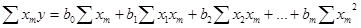 .
.
ІІ етап. Оцінка лінії регресії.
Оцінками лінії регресії є теоритичні значення – У.
Обчислимо параметри рівняння регресії, яке описує зв”язок продуктивності праці з такими показниками:
1)урожайністю;
2) витратами добрив.
Позначимо урожайність 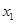 , витрати добрив
, витрати добрив  , продуктивність праці - у. Для нашого прикладу лінійне рівняння регресії матиме вигляд:
, продуктивність праці - у. Для нашого прикладу лінійне рівняння регресії матиме вигляд:
 .
.
Складемо систему нормальних рівнянь.
6604,4 = 20  + 2024
+ 2024 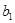 +95;
+95;
734192,89 = 2024  +242806,96
+242806,96 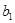 +10474,55
+10474,55 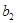 ;
;
32986,13 = 95  + 10474,55
+ 10474,55 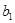 +508,98
+508,98 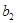 .
.
Розв язання системи дає таке лінійне рівняння:
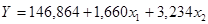 .
.
Отже, із збільшенням урожайності на 1 ц/га продуктивність праці збільшиться на 1,66 ц/особу за умови, що витрати добрив залишаються незмінними. Частинний коефіцієнт регресії при 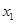 1,660 нижчий від коефіцієнта при цій змінній у парній моделі - 1,733. Частинний коефіціент регресії при
1,660 нижчий від коефіцієнта при цій змінній у парній моделі - 1,733. Частинний коефіціент регресії при  3,234 показує середній приріст продуктивності праці при збільшенні витрат добрив на 1 тис.грн. за умови незмінної урожайності. Якщо обчислити параметри ленійного рівняння парної регресії
3,234 показує середній приріст продуктивності праці при збільшенні витрат добрив на 1 тис.грн. за умови незмінної урожайності. Якщо обчислити параметри ленійного рівняння парної регресії 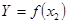 дістанемо
дістанемо  = 197,300 + 27,979
= 197,300 + 27,979 . Парна регресія показує прямий зв”язок між витратами добрив і продуктивністю праці. Причина розбіжностей частинних і парних коефіцієнтів регресій полягає у взаємозв”язку факторних ознак
. Парна регресія показує прямий зв”язок між витратами добрив і продуктивністю праці. Причина розбіжностей частинних і парних коефіцієнтів регресій полягає у взаємозв”язку факторних ознак 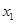 і
і  .
.
Передумову багатофакторного регресійного аналізу про можливість зміни кожного фактора окремо при незмінності інших факторних ознак на практиці здійснити важко. Як правило, зміна значень одного фактора викликає явні зміни у всій сестемі взаємозв”язаних факторів. Більш поглибленний статистичний аналіз взаємозв”язку факторів можливий при використанні систем рівнянь регресії (рекурентні системи).
Так за данними табл. 1 обчислені багатофакторні та парні регресійні моделі
 = 154,840+1,733
= 154,840+1,733 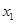
 = 197,300+27,979
= 197,300+27,979 
 = 146,864+1,660
= 146,864+1,660 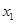 +3,234
+3,234 
Залежність 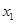 від
від  можна описати рівнянням
можна описати рівнянням
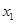 =30,394+14,906
=30,394+14,906  .
.
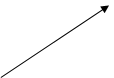
Схематично взаємозв язки трьох ознак зображено на рис 1.

 3,234 1,660
3,234 1,660
 |


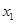
14,906
Рис. 1. Схема зв”язку трьох ознак.
Стрілки показують напрям зв”язку, цифри над стрілками – відповідно коефіцієнти регресії: частинні для пар 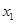 -
-  та
та  -
-  і парні для
і парні для  -
- 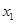 .
.
В обстеженій сукупності господарств збільшення витрат добрив на 1 тис.грн. приводить до збільшення продуктивності праці на 3,234 ц/особу, що було б правильно, якби при цьому залишилась незмінною урожайність. Насправді ж зі збільшенням витрат добрив урожайність збільшилась на 14,906 ц /га. Оскільки з підвищенням урожайності на 1 ц/га. відповідно збільшиться продуктивність праці на 1,66 ц/особу, то підвищення урожайності на 14,906 ц /га. відповідно збільшить продуктивність праці на 24,744 ц/особу, тобто на 1,66*14,906 = 24,744. Таким чином, вплив фактора  – це сума двох складових частин: безпосереднього впливу
– це сума двох складових частин: безпосереднього впливу 
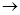
 і опосередкованого -
і опосередкованого - 
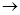
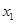
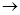
 . Слід зауважити, що повний вплив (повний коефіцієнт регресії) збігається з парним коефіціентом регресії
. Слід зауважити, що повний вплив (повний коефіцієнт регресії) збігається з парним коефіціентом регресії  на
на  (27,979). Розглянутий приклад - найпростіший випадок систем рівнянь регресії, які називаються рекурентними. Вони являють собою ефективний метод аналізу структури причинно-наслідкових зв”язків.
(27,979). Розглянутий приклад - найпростіший випадок систем рівнянь регресії, які називаються рекурентними. Вони являють собою ефективний метод аналізу структури причинно-наслідкових зв”язків.
ІІІ етап. Оцінки тісноти зв”язку.
Тісноту зв”язку між результативною ознакою та сукупністю факторних ознак визначають за допомогою сукупного коефіцієнта детермінації.
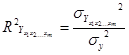 ,
,
де 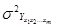 - теоретична дисперсія багатофакторного рівняння регресії.
- теоретична дисперсія багатофакторного рівняння регресії.
Сукупний кофіцієнт детермінації характеризує частку варіації результативної ознаки, яка лінійно пов”язана з варіацією включених у рівняння регресії факторних ознак.
Теоретичну дисперсію обчислюють за формулою
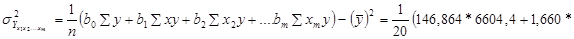
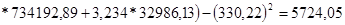 .
.
Сукупний коефіцієнт детермінації
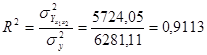 .
.
Таким чином, у обстеженій сукупності господарств 91,13% варіації продуктивності праці лінійно пов”язані з різним рівнем урожайності та витрати добрив.
Визначення зв”язку в моделях множинної регресії доповнюється оцінкою тісноти зв”язку з кожною факторною ознакою окремо. Для цього застосовують частинні коефіцієнти детермінації.
Для розрахунку цих коефіцієнтів для зв”язку у і 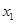 порівняємо дві регресійні моделі: рівняння з двома ознаками
порівняємо дві регресійні моделі: рівняння з двома ознаками 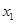 і
і  та рівняння без ознаки
та рівняння без ознаки 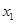 . Дві факторні ознаки пояснюють 91,13% варіації ознаки
. Дві факторні ознаки пояснюють 91,13% варіації ознаки  (коефіцієнт детермінації
(коефіцієнт детермінації 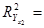 0,3590). Таким чином, введення в модель ознаки
0,3590). Таким чином, введення в модель ознаки 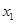 пояснює додатково 55,23 % варіації ознаки
пояснює додатково 55,23 % варіації ознаки  .
.
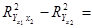 0,9113 – 0,3590 = 0,5523.
0,9113 – 0,3590 = 0,5523.
Оскільки ознака  пояснює 35,9% варіації ознаки
пояснює 35,9% варіації ознаки  , то 64,1% варіації залишається непоясненою, тобто
, то 64,1% варіації залишається непоясненою, тобто

Це максимально можлива частка варіації, яку може пояснити додатково введена в рівняння регресії факторна ознака 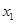
Відношення додатково поясненої варіації до максимально можливої і є частиним коефіцієнтом детермінації ознаки 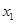 . Його визначають так:
. Його визначають так:
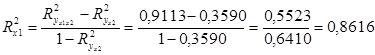 .
.
Отже, варіація урожайності пояснює 86,16% варіації продуктивності праці, непоясненої фактором  (витратами добрив).
(витратами добрив).
Частинний коефіцієнт детермінації ознаки  обчислюється так:
обчислюється так:
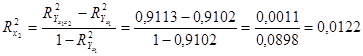 .
.
Лише 1,22% варіації продуктивності праці додатково пояснюється варіацією витрат добрив.
IV етап перевірки істотності зв’язку.
Його здійснюють з допомогою двох критеріїв математичної статистики:
- F – критерію;
- коефіцієнтів детермінації;:
- критерію Стьюдента 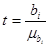 .
.
Для частинного коефіцієнта детермінації число ступенів вільності 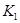 =1.
=1.
Для сукупного коефіцієнту детермінації 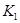 = m -1=3-1=2;
= m -1=3-1=2; 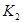 = n-m =
= n-m =
20-3=17. Для рівня істотності 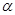 =0,05 критичне значення R20.95(2,17) = 0,297.
=0,05 критичне значення R20.95(2,17) = 0,297.
Фактичне значення 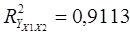 значно перевищує критичне, тому істотність зв’зку результативної ознаки з обома факторами доведена.
значно перевищує критичне, тому істотність зв’зку результативної ознаки з обома факторами доведена.
Розглянемо істотність зв’язку з кожною з факторних ознак окремо. Для частинного коефіцієнта детермінації критичне значення R20.95(1,17) = 0,208. Для ознаки 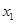 фактичне значення
фактичне значення 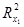 =0,8616 більше від критичного, що свідчить про істотність частинного зв’язку
=0,8616 більше від критичного, що свідчить про істотність частинного зв’язку 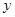 з
з 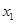 . Для ознаки
. Для ознаки 
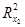 = 0,0122 менше від критичного і наявність частинного зв’язку
= 0,0122 менше від критичного і наявність частинного зв’язку 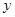 і
і  не доведена.
не доведена.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2483; Нарушение авторских прав?; Мы поможем в написании вашей работы!