Функція БЗ

Розрахунки на основі постійної процентної ставки.

Визначення майбутньої вартості

Поняття майбутньої вартості базується на принципі нерівноцінності грошей, які відносять до різних моментів часу. Вкладення, зроблені сьо­годні, у майбутньому складуть велику величину. Ця група функцій дозво­ляє розрахувати:

♦ майбутню або нарощену вартість серії фіксованих періодичних
платежів, а також майбутню вартість поточного значення або вне­
ску позики при постійній процентній ставці (функція БЗ);

♦ майбутнє значення інвестиції після нарахування складних відсотків
при змінній процентній ставці (функція БЗРАСПИС).

Функція БЗ розраховує майбутню вартість періодичних постійних платежів і майбутнє значення єдиної суми або внеску позики на основі постійної процентної ставки.

Синтаксис Б3(норма, число_периодов, выплата, нз, тип).

Значення, що повертає функція БЗ, - це аргумент fv формули (1).

Розглянемо різні варіанти використання цієї функції при розв'язу­ванні конкретних задач.

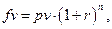(3)

fv — майбутня вартість внеску або позики;

pv — поточна вартість внеску (позики);

n — загальна кількість періодів нарахування відсотків;

r — процентна ставка по внеску (займу).

Ця формула відповідає класичній формулі розрахунку нарощеної суми внеску по методу складник відсотків.

Для обчислення майбутнього значення єдиної суми використовують-.] ся аргументи нз, норма, число_периодов. У цьому випадку на робочому листі EXCEL формула прийме вигляд:

= Б3(норма, число_периодов, нз).

При розв'язуванні конкретної задачі замість назв аргументів доціль­но записати відповідні числа або адреси клітинок, в яких знаходяться ці

числа.

2. Розглянемо ситуації, коли платежі проводяться систематично, а не один раз, як у попередньому прикладі. Ці платежі можуть здійснюватися на початку кожного розрахункового періоду (так звані платежі пренумеран-до) або наприкінці (постнумерандо) протягом п періодів. Нехай в кожному періоді вноситься однакова сума. Потрібно знайти сукупну величину таких вкладень (їхню майбутню вартість) наприкінці п-го періоду для обох ви­падків. Відмінність у розрахунку при цьому полягає в тому, що в другому випадку не відбувається нарахування відсотків на останній внесок, тобто усі внески пренумерандо збільшуються на складні відсотки на один розра­хунковий період більше, ніж внески постнумерандо.

2.1. Для розрахунку майбутньої вартості серії фіксованих періодич­них платежів, якщо вони вносяться на початку кожного періоду (так звані "обов'язкові платежі" або пренумерандо), використовується формула:

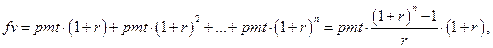(4)

де f_v — майбутня вартість серії фіксованих періодичних платежів;

pmt — фіксована періодична сума платежу;

п — загальна кількість періодів виплат;

r — постійна процентна ставка.

При розрахунку за допомогою функції БЗ використовуються аргу­менти: норма, число_периодов, выплата; тип = 1. У загальному випад­ку формула має вигляд:

= Б3(норма, число_периодов, выплата,,1).

Результат повинен збігатися з розрахунком по формулі (4).

2.2. Для розрахунку майбутньої вартості серії фіксованих періо­дичних платежів, якщо виплати відбуваються наприкінці періоду (так на­звані "звичайні платежі" або постнумерандо), формулу (3) слід моди­фікувати:

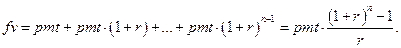(5)

Відповідний розрахунку по формулі (5) запис на робочому листі EXCEL має вигляд:

= БЗ{норма, число_периодов, выплата,, 0).

Так як аргумент тип = 0, то можна опустити останні параметри і записати:

= Б3(норма, число_периодов, выплата),

підставивши замість аргументів відповідні числа або адреси клітинок, в яких знаходяться ці числа.

Дата добавления: 2014-01-07