Автономный риск

Будущая доходность какого-либо актива как правило величина случайная. Ее конкретное значение зависит от множества случ.событий. в математике существует аппарат, позволяющий учитывать влияние случ.будущего на числовые значения тех или иных показателей. Это матем. аппарат теории вероятности.

Доходность с матем.точки зрения – случайная величина, т.е. измеримая функция от множества элементарных событий, мерой которого является вероятность.

Выделяют 2 вида случ. Величин: дискретные (кол-во возможных исходов можно посчитать) и непрерывные (множество значений имеет мощность сплошiного континуально)

При описании риска в эк.задачах используют характеристики случайных величин такие как дисперсия, среднеквадратического отклонение. Если доходность актива дискретная величина, то ее дисперсия определяется по формуле:

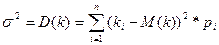,где

n – количество возможных значений дискретной случ.величины доходности (может быть бесконечным)

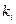- i-ое возможное значение случ.величины доходности акции

М(к) – мат.ожидание случ.величины доходности акции

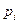- вероятность i-ого значения случ.величины доходности акции

Среднеквадратическое отклонение доходности: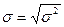

Дисперсия непрерывной случ.величины рассчитывается по формуле:

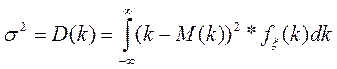, где

- Значение функции плотности вероятности непрерывной случ.величины

M(k) – мат.ожидание

к- доходность акции

Мат.ожидание в случае с дискретной величиной:

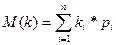
В случае с непрерывной случ.величиной:

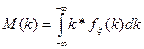
Для определения этих показателей (дисперсии и среднекв.отклонения) необходимо знать распределение вероятности дискретной случ.величины, либо функцию плотности вероятности (закон распределения вероятности непрерыв. случ.величины). на практике не первое ни второе изначально неизвестно. Поэтому прибегают к стат.методам опред-я этих показателей. Как правило имеют дело с временными рядами доходности активов. Временной ряд доходности должен обладать при этом признаками траектории эргодического стационарного случ.процесаа – независимость его сечений(случ.величина в конкрет.момент времени рассм.периода) эргодичность устанавл.гипотезой эффективности фин.рынков, кот. утвержает что изменение цен ценных бумаг не зависит от изменения цен в прошлом.

Стационарным процессом в узком смысле называют такой процесс, множество сечений которого имеет одинаковый закон распределения вероятности. Проверка процесса на стационарность осуществляют разбивая рассматриваемый временной ряд на несколько временных рядов и проверяя гипотезу о законе распределения вероятности сечения процесса на каждом малом временном ряде.

Если процесс обладает характеристиками стационарности и эргодичности, то для оценки дисперсии и среднекв.отклонения его сечения можно применять выборочный стат.метод. Стат. оценка дисперсии и среднекв.отклонения должна удовлетворять трем требованиям:

1) Она должна быть несмещенной (мат.ожидание оценки = оцениваемый параметр)

2) Оценка должна быть состоятельной, т.е. сходится по вероятности к оцениваемому параметру

3) Оценка должна быть эффективной; среди всех несмещ.оценок ожна должна обладать наим.дисперсией. Несмещ. оценкой мат.ожидания явл. выборочная средняя.

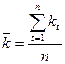, где

n – количество значений доходности в выборке

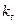- t-ое значение доходности актива

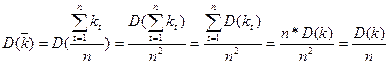
Рассмотрим выборочную дисперсию:

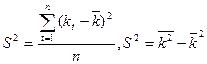
Рассмотрим мат.ожидание:

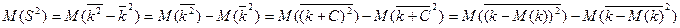
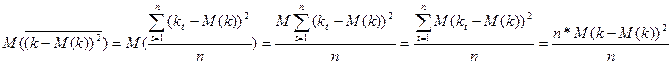=D(k)

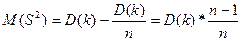
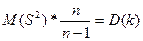
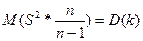
Мат.ожидание оценки 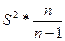=дисперсии величины к, т.е. доходности акции.

И следовательно эта оценка является несмещенной и состоятельной оценкой дисперсии. Она называется исправленной выборочной дисперсией =

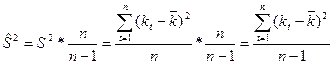
Среднекв.отклонение вычисляется так: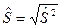

Исправленная выборочная дисперсия не является эфф.оценкой дисперсии рассмотренной величины, т.к. существует оценка имеющая меньшую дисперсию:

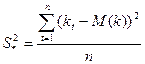
Получение такой оценки на практике как правило невозможно, т.к. мат.ожидание предварительно неизвестно.

Для оценки автономного риска также применяют относительные показатели: коэффициент вариации:

Наилучшей оценкой которого явл.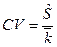

Дата добавления: 2014-01-06