Риск и доходность: теория портфеля и модели оценки активов

В 1952 году Г. Марковец опубликовал фундаментальную работу Portfolio Selection, в которой описал модель выбора оптимального портфеля инвестором.

Процесс выбора Марковец моделировал при помощи специальной функции математического ожидания доходности от её среднеквадратического отклонения, график каждой из которой содержал множество пар (математическое ожидание доходности, риск), которые имели для конкретного инвестора одинаковую полезность, т.е. инвестору безразлично какую из пар предпочесть, если они принадлежат к графику одной и той же функции.

Схема такого графика имеет вид кривой, поэтому её часто называют кривой безразличия.

Где f₁, f₂, f₃ – это 1, 2, 3 функции кривых безразличия конкретного инвестора. Они отличаются между собой только параметром смещения по вертикальной оси. Наклон этих кривых при любых одинаковый.

Исходные предпочтения построения кривых безразличия, явл.:

1. При заданном уровне риска (среднеквадратическое отклонение доходности) инвестор предпочтет портфель с большей ожидаемой доходностью (математическое ожидание доходности).

2. При заданном уровне ожидаемой доходности инвестор предпочтет тот портфель, который имеет меньший риск.

Наилучшим портфелем для инвестора, руководствующегося двумя вышеназванными принципами выбора (ненасыщаемости и избегание риска) будет портфель лежащий на самой высокой кривой безразличия.

Если бы инвестору были доступны любые сочетания доходности и риска, то инвестор бы выбрал портфель при таких условиях: с бесконечно большой ожидаемой доходностью и бесконечно малым риском.

Однако его инвестиционные возможности ограничены достижимым множеством инвестиционных портфелей.

Инвестор руководствуется двумя принципами выбора, нет смысла искать оптимальный портфель среди всех портфелей достижимого множества.

Выбирать нужно из множества портфелей, отвечающих одновременно двум требованиям:

1. При каждом уровне риска в данное множество включаются портфели с наибольшими ожидаемыми доходностями.

2. При каждом уровне ожидаемой доходности, есть портфель с минимальным риском, который должен быть включен в данное множество.

Множество портфелей, отвечающее двум этим требованиям, называют эффективным множеством портфелей.

Одновременно двум этим условиям удовлетворяет левая граница СВ достижимого множества.

Процесс выбора продемонстрирован на следующем рисунке.

Оптимальным портфелем будет касательный портфель «О», которой по сравнению с другими портфелями из эффективного множества расположен на самой высокой кривой безразличия.

В развитии теории инвестиционного портфеля поучаствовал Дж. Тобин, который ввел в теорию безрисковый актив.

Безрисковый актив – это актив будущая доходность инвестиций в котором точно определена (не является случайной величиной).

Саму доходность безрискового актива, называют безрисковой доходностью (k_RF).

Инвестирование в безрисковый актив, называют безрисковым кредитованием.

Рассмотрим ожидаемую доходность портфеля, представляет собой комбинацию безрискового актива (RF) и рискового портфеля (i), т.е. комбинированный портфель (р).

Рассмотрим ожидаемую доходность:

Рассмотрим дисперсию доходности комбинированного портфеля:

Найдем зависимость математического ожидания доходности комбинированного портфеля. Для этого необходимо:

1) => 0

2) =>

Как видно из формулы зависимость ожидаемой доходности комбинированного портфеля от его риска линейная.

Продемонстрируем влияние безрискового кредитования на эффективное множество потрфелей, изобразим схему графика данной функции.

В результате комбинирования Т с безрисковым активом , получаем новую эффективную границу, отвечающую двум требованиям, предъявленную к эффективному множеству портфелей.

Дальнейшим шагом в развитии теории было введение предположения о возможности инвестора неограниченного заимствования под безрисковую ставку .

Рассмотрим доходность портфеля p, сформируем целиком за счет собственных средств и займов из рискового портфеля i.

Рассмотрим эту ситуацию:

Где -вложения в рискованный портфель i;

- собственные инвестиции инвестора;

- заемные средства, вложенные в портфель.

Доходность собственных вложений инвестора:

Где - коэффициент финансового рычага.

=>

Рассмотрим, как безрисковое заимствование сказывается на эффективном множестве.

- эффективное множество Марковица

Эффективное множество портфелей приобретет вид прямой линии проходящей через касательный портфель Т.

Уравнение этого эффективного множества приведено на рисунке.

Где -ожидаемая доходность эффективного портфеля;

- безрисковая доходность;

-ожидаемая доходность касательного портфеля Т из эффективного множества Марковица.

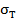- среднеквадратическое отклонение доходности касательного портфеля Т.

Оптимальный портфель выбираемый инвестором зависит от его предпочтений относительно доходности и риска и от формы кривой безразличия (на рисунке это портфель «О»). Для инвестора оптимальный портфель, является комбинация касательного портфеля Т и безрискового кредитования или заимствования.

Эта модель не позволяет судить о ценообразование на рынке капитала, так как на практике у всех инвесторов разный период владения инвестициями (могут отличаться безрисковые ставки), разные прогнозы математических ожиданий и дисперсий, а так же ковариаций доходностей отдельных ценных бумаг (различные эффективные множества Марковица).

Дата добавления: 2014-01-06