Модель оценки капитальных активов

Эта модель является макроэк. обобщением теории инвестиционного портфеля и разработана нобелевским лауреатом Шарпом.

В основе этой модели 10 предположений:

1. инвесторы оценивают активы исходя из их ожидаемых доходностей, дисперсий и ковариации доходности

2. все инвесторы одинаково оценивают ожидаемые доходности, дисперсии и ковариации доходности активов

3. период владения всех инвесторов одинаковый

4. частные активы бесконечно делимы

5. инвесторы имеют возможность давать в долг и заимствовать под безрисковую ставку

6. ставка безрисковых заимствований совпадает со ставкой безрискового кредитования

7. безрисковая ставка одинакова при всех инвесторах

8. налоги не сущ

9. транзакционные издержки (затраты на совершение операций с ценными бумагами) не сущ

10. вся информация, сказывающаяся на ценах ценных бумаг, не замедлительно доступна всем инвесторам без затрат на ее получение

Сделанные предположения позволяют утверждать, что все инвесторы выбирают свои оптимальные портфели из одного и того же эффективного множества.

Касательная портфеля М наз рыночный портфель

Все инвесторы выбирают оптимальный портфель, комбинируя его с безрисковым заимствованием и кредитованием.

Как утверждает Шарп, рыночные портфель – это портфель составленный из всех активов, кот есть на рынке, причем доля каждого актива соответствует его относительной рыночной стоимости.

Относительная рыночная стоимость актива – это отношение его суммарной рыночной стоимости к суммарной стоимости всех активов на рынке.

Уравнение рынка капитала имеет вид:

С использованием этой формулы Шарп получил формулу ожидаемой доходности ценных бумаг конкретного вида, кот имеет место быть при равновесном состоянии фондового рынка.

Шарп рассмотрел портфель предст собой комбинацию рын портфеля и i-ой рискованной ценной бумаги. Доходность такого портфеля описывается формулой:

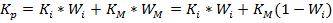
,– доходности ценной бумаги I и рыночного портфеля соответственно

, - доли инвесторов в ценных бумагах i и рыночный портфель в общей их сумме

Математическое ожидание доходности:

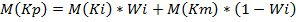
Дисперсия доходности комбинированного портфеля равна:

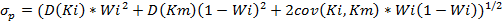
Эта формула в совокупности с формулой математического ожидания доходности портфеля можно рассматривать как функцию математического ожидания доходности от ее среднеквадратического отклонения, заданную параметрически (параметр Wi).

График этой функции в системе координат доходность;риск выглядит так:

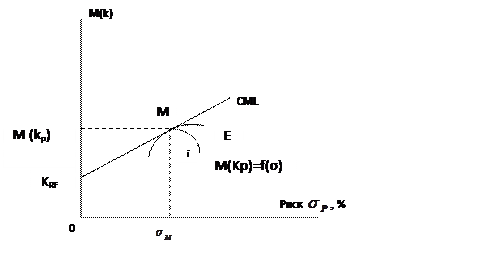
Так как E- эффективная граница, содержащая крайний портфель (с max доходностью и min риском), то точка М – точка касания линии CМi не только эффективного множества, но и кривой iM. Это означает,что наклон кривой iM в точке M должен совпадать с наклоном CМi.

Для нахождения наклона (tg угла) кривой iM в точке М продифференцируем функцию ожидания доходности комбинированного портфеля от его риска.

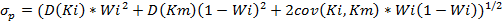
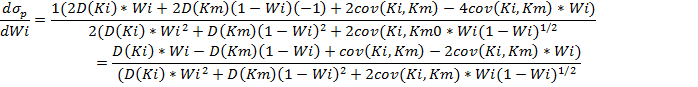
В точке M значение параметра Wi=0 – нулевая доля ценной бумаги i. Найдем производную в точке M.

Данное значение должно равняться угловому коэффициенту CML.

(*)

Как видно из этой формулы, ожидаемая доходность ценной бумаги i зависит только от ее ковариации с доходностью рыночного портфеля, который в эк смысле явл мерой риска, вложенного ценной бумагой i в рын портфель, которым обладает каждый инвестор, сочетается с безрисковым кредитованием или заимствованием. Она является мерой портфельного риска ценной бумаги, от которой зависит ее ожидаемая доходность

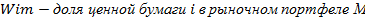
Зависимость, описанная формулой (*) может быть представлена графически

Линия рынка ценной бумаги имеет и др представление через коэффициент β. Принимая во внмание, что выполняется равенство , можно записать β-версию SML:

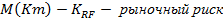
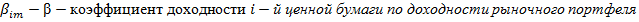
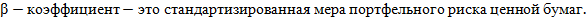
Если риск рын портфеля принять за 1, то выполняется равенство:

Графическое представление β-версии SML

β-коэффициент произвольного портфеля ценной бумаги по доходности рын портфеля вычисляется по такой формуле:

-количество видов ценных бумаг, входящих в произвольный портфель

- β-коэффициент доходности i-й ценной бумаги по доходности рыночного портфеля

Wi-доля i-й ценной бумаги в общей стоимости произвольного портфеля p

Дата добавления: 2014-01-06