Уравнение неразрывности

Общие уравнения сплошной среды

Рассмотрим случай, когда невязкая жидкость течет по горизонтальной цилиндрической трубе с изменяющимся поперечным сечением.

Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.

Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы.

Пусть скорости стационарного течения жидкости через сечения трубы S₁ и S₂ равны соответственно v₁ и v₂. Объем жидкости, протекающей за промежуток времени t через сечение S₁, равен V₁=S₁v₁t, а объем жидкости, протекающей за то же время через сечение S2, равен V₂=S₂v₂t. Из равенства V₁=V₂ следует, что

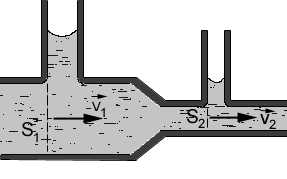Рис 1.14

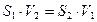(1.27)

Соотношение (1.27) называют уравнением неразрывности. Из него следует, что Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.

Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь S поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид:

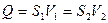(1.28)

Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях.

Дата добавления: 2014-01-07