Числовые параметры распределения дискретных и непрерывных случайных величин

Непрерывной случайной величины

Числовым параметром, определяющим положения рассеяния дискретных величин, являются среднее арифметической значение

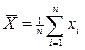
Численное значение среднего арифметического находится из опытных данных результата измерений.

Для непрерывной случайной величины аналогом среднего арифметического является математической ожидание, которое представляет собой определенный интеграл от произведения плотности вероятности φ(x) на действительное переменное, взятое в пределах от - ∞ до + ∞:

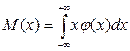
Кроме математического ожидания характеристикой положения является мода.

М_О (x) – значение случайной величины с наибольшей вероятностью и медиана М_Е (x) – значение случайной величины, при которой площадь кривой распределения делится пополам.

Характеристикой рассеяния (мерой рассеяния) случайных дискретных величин является дисперсия:

,

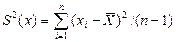где n – число измерений.

Для непрерывной случайной величины дисперсия определяется по формуле

.

Практическую значимость получила величина среднеквадратичного отклонения, которая для дискретных величин обозначается S = +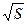² и представляет собой положительное значение корня квадратного из дисперсии.

Для непрерывных величин аналогом S является среднее квадратичное отклонение σ = +.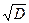

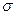При опытно-статистическом анализе для непрерывных величин принято говорить как о генеральной совокупности, а для дискретных величин о выборочных значениях. Поэтому параметры и определяют характеристики рассеяния непрерывной случайной величины, а величины 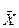и S – параметры рассеяния по данным выборки (для дискретных величин). Необходимо четко проводить разграничение: математическое ожидание и среднее квадратичное отклонение 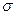понимаются как постоянные, но неизвестные величины, характеризующие теоретическое распределение (генеральную совокупность); значения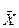и S понимаются как случайные величины, определенные из выборочных наблюдений. 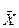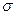Чем больше объем выборки, тем меньше разница между и , и S.

Согласно центральной предельной теореме теории вероятностей получено соотношение

,

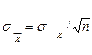где 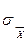– среднее квадратичное отклонение среднего арифметического;

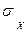– среднее квадратичное отклонение случайной величины.

Эта формула отражает фундаментальный закон теории погрешностей, из которого следует, что при необходимости повышения точности измерений в 2 раза, необходимо число измерений увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз. При 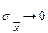, что означает приближение среднего арифметического ряда измерений к его математическому ожиданию.

Дата добавления: 2014-01-07