Свободные колебания систем с бесконечным числом степеней свободы

Рассмотрим общий подход на примере простой шарнирно опертой балки:

EI=const

m=const

Массу балки зададим её интенсивностью на единицу длины.

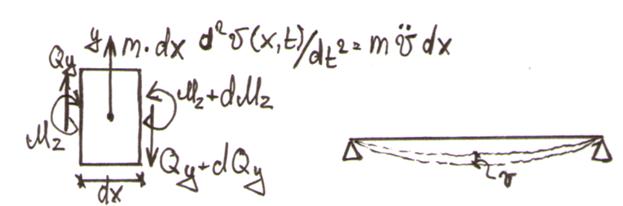
Рассмотрим колебания балки относительно положения статического равновесия, которое она принимает под действием сил тяжести. Поэтому в уравнении движения сил тяжести и упругих сил от их действия учитывать не будем как взаимно уравновешивающие.

В первом приближении не будем учитывать силы неупругого сопротивления.

Спроецируем на Y:

Уравнение в частных производных IV порядка с постоянными коэф.-ми: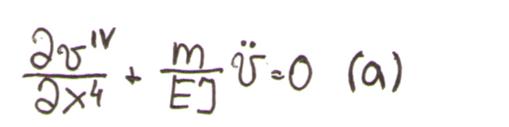

Решение этого уравнения запишем в виде:

Подставляя (б) в (а) и сокращая на sin(kt+β),получим следующее обыкновенное уравнение IVпорядка

Обозначим

Сложим 2) и 4)

Для частного уравнения (78) решение имеет вид:

Подставим в (г)

Частота собственных колебаний шарнирно опертой балки

Спектр шарнирно опертой балки представляет собой набор частот, количество которых является бесчисленным, при этом высшие частоты отстоят от низших на всё более увеличенном расстоянии.

Низшая частота – основная

Остальные (высшие) – обертоны.

Каждой собственной частоте соответствует собственная форма колебаний, вид которой получается из формулы (77).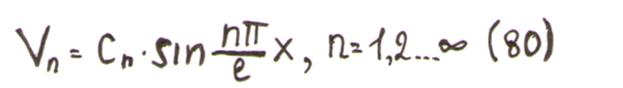

Постоянная С может быть принята равной любому значению, и форма определяется значением величины n в формуле.

Амплитуда колебаний при свободных движениях (при отсутствии нагрузки) зависит от начальных условий, при этом должны быть заданы начальная скорость и начальное перемещение.

Свободные движения для балки складываются из составляющих, отвечающих одной из собственных форм и частот.

Для систем с бесконечным числом степеней свободы справедливо понятие ортогональности собственных форм, однако, оно здесь превращается в интегральное соотношение: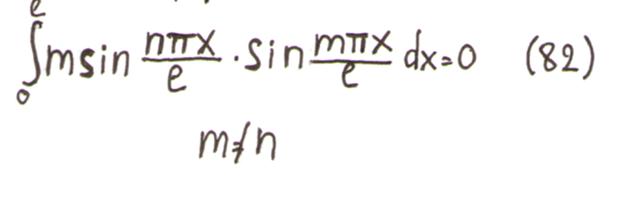

Для вычисления нормирующего множителя вычисляется интеграл по формуле (82) при m=n.

Для любой собственной формы Bn=ml/2 (83) - нормирующий множитель.

При реализации в натуральных условиях обычно реализуются только несколько низших собственных частот.

Сопоставим частоту в балочной конструкции.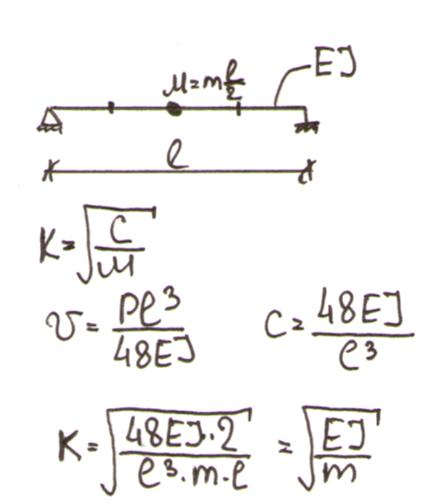

Дата добавления: 2014-01-06