Колебания мостовых конструкций при подвижной нагрузке

Лекция № 15

При движении автомобилей по мостовым конструкциям возникают колебания, причиной которых является наличие скорости.

Постановки задачи расчёта зависят от учёта инертности мостовой конструкции и инертности подвижной нагрузки.

1)Инертность нагрузки и мостовой конструкции не учитывается, а учитываются только фактические движения.

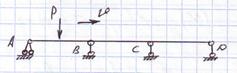
Эта задача рассматривается в статике сооружении с использованием линий влияния

2)Инертность мостовой конструкции учитывается, а подвижной нагрузки не учитывается(задача А.Н.Крылова).

3)Инертность нагрузки учитывается, а мостовой конструкции не учитывается.

(Задача Виллиса-Стокса)

4)Инертность нагрузки и мостовой конструкции учитываются.

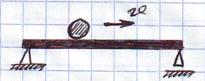
(Задача Инглиса-Белотина)

5)Учитывается инертность нагрузки и мостовой конструкции, а для нагрузки учитывается её подрессоренность (упругое опирание на дорогу).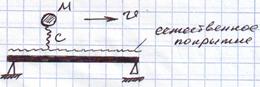

(Задача Моргаевского)

Задача Крылова.

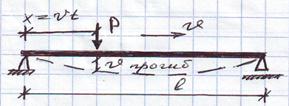EI=const; m=const

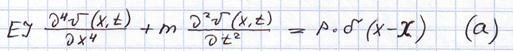
Это уравнение 2-го порядка решается методом разделения переменных по правилу Коши.

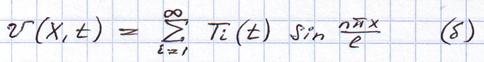
Подставим (б) в (а), а затем выполним преобразование уравнения путём его интегрирования в пределах длины балки после умножения на одну из собственных форм.

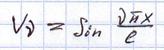собственная форма.

При этом учитывается, что собственные формы между собой ортогональны, уравнение становится такого вида:

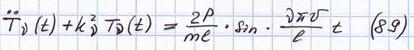
частота возмущения.

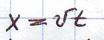
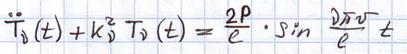
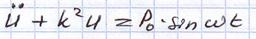
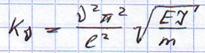частота собственных колебаний балки.

Полученная система уравнений представляет собой независимую систему д.у. 2-го порядка с правой частью. Решение для этого уравнения складывается из свободных колебаний с собственной частотой и вынужденных колебаний с частотой возмущения.

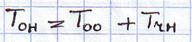
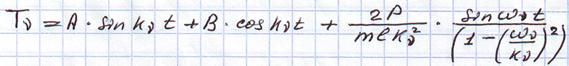
Для определения А и В учтём начальные условия:

1)При t=0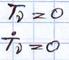

1.0=В*1 следовательно В=0

2.

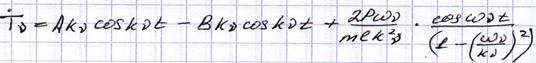
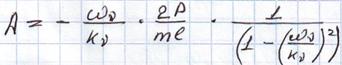
Проанализируем (91): при совпадении собственной частоты балки с частотой возмущения амплитуды возмущений растут, следовательно при движении нагрузки возможны критические скорости, при которых балка может получать большие перемещения.

Вычислим критическую скорость движения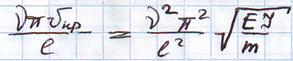

При

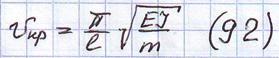
Пример:

Вычислим критическую скорость для моста с м

Приближенно для широкого класса мостовых сооружений период низшей собственной формы равен:

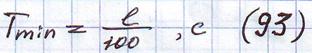
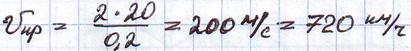
Для реальных скоростей движения критические скорости недостижимы.

Дата добавления: 2014-01-06