Момент инерции

В этом пункте обсудим физический смысл и некоторые свойства введенной в предыдущем пункте 4.1 величины 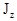- момента инерции твердого тела относительно данной оси.

Уже в самом названии величины 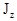скрывается ее смысл, который легко понять, рассмотрев основное уравнение (4.7). Действительно, поскольку это уравнение имеет такой же формальный вид, что и второй закон Ньютона, то момент инерции твердого тела относительно данной оси можно трактовать как количественную меру инертности тела относительно этой оси.

Здесь следует отметить, что некоторые студенты ошибочно считают момент инерции мерой инертности тела при вращательном движении твердого тела относительно данной оси. В действительности же, момент инерции тела относительно данной оси существует независимо от того, вращается ли данное тело или нет. При вращательном движении твердого тела мы наблюдаем одно из частных, конкретных проявлений этого свойства инертности, так же как, например, масса тела, существуя независимо от характера движения тела, играет роль инертности тела при его поступательном движении.

Рис. 4.2

В тех случаях, когда дискретностью вещества можно пренебречь, считают, что в объеме твердого тела вещество распределено непрерывно. Это позволяет при вычислении момента инерции тела использовать интегральное исчисление.

Твердое тело “разбивают” на элементарно малые (рис. 4.2) участки объемом dV, такие, что их можно считать материальными точками. Распределение вещества внутри объема тела можно характеризовать величиной

, (4.8)

которая называется плотностью в малой окрестности dV данной точки тела.

Выразив элементарную массу dm с помощью (4.8) , определение (4.4) запишем в виде

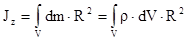, (4.9)

где суммирование по всем материальным точкам заменено интегрированием по объему твердого тела. В соотношении (4.9) величина определяет расстояние от элементарного объема dV до оси, относительно которой вычисляется момент инерции тела. В общем случае величины и R являются функциями положения элементарного объема (например, декартовых координат x, y, z). Для однородного тела и поэтому вычисление момента инерции тела упрощается:

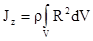. (4.10)

Из соотношений (4.4), (4.9) и (4.10) видно, что величина момента инерции тела относительно данной оси существенным образом зависит не столько от общей массы тела, сколько от того, как эта масса распределена относительно данной оси.

Во многих случаях вычисление момента инерции тела относительно произвольной оси еще более упрощается, если использовать теорему Штейнера:

Момент инерции тела J относительно произвольной оси равен сумме момента инерции тела J₀ относительно оси, проходящей через центр инерции тела параллельно данной, и произведения массы тела m на квадрат расстояния 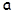между этими осями:

. (4.11)

Докажем справедливость этого утверждения.

Рис. 4.3

На рис. 4.3 произвольная ось, проходящая через точку А, и ось, проходящая через центр инерции 0, перпендикулярны к плоскости чертежа.

Легко видеть, что радиус-вектор 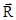, определяющий положение элементарной массы dm относительно произвольной оси А, как следует из рис. 4.3, имеет очевидный вид:

Вычислим квадрат модуля этого вектора, входящий в подынтегральное выражение в (4.9):

Подставим это соотношение в (4.9) и представим интеграл в виде суммы трех интегралов:

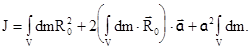
Постоянные величины вынесены за знак интеграла. В последнем соотношении интеграл в скобках во втором слагаемом равен 0. Этот результат непосредственно следует из определения центра инерции (3.5), записанного для сплошного тела в интегральной форме:

.

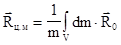В данном случае , так как ось 0 проходит именно через центр инерции тела. С учетом этих соображений выражение для примет вид

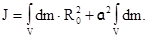
В соответствии с (4.9) первый интеграл определяет момент инерции тела относительно оси, проходящей через его центр инерции, то есть 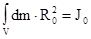. Второе же слагаемое, в силу очевидного равенства , где m - масса всего тела, примет вид

.

Окончательно для J имеем

.

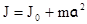Теорема Штейнера доказана.

Выводы: Момент инерции тела относительно данной оси является количественной мерой инертности этого тела относительно этой оси. Величина момента инерции зависит как от массы тела, так и от характера распределения этой массы относительно оси.

Контрольные вопросы.

4.2. Как изменится угловое ускорение материальной точки, вращающейся по окружности под действием постоянной по величине касательной силы, если, не меняя эту силу, увеличить радиус окружности? Какой фактор оказывает большее влияние на результат: увеличение момента касательной силы или увеличение момента инерции материальной точки?

Дата добавления: 2014-01-07