Примеры вычисления моментов инерции однородных симметричных тел

В этом пункте приведем примеры вычисления моментов инерции относительно оси, проходящей через центр масс, для некоторых однородных тел правильной геометрической формы, а также некоторые результаты, часто встречающиеся при решении конкретных задач.

а) Рассчитаем момент инерции однородного сплошного цилиндра относительно его оси симметрии 00 (рис. 4.4), который имеет массу m, радиус R и высоту h.

Разобьем цилиндр на соосные с ним цилиндрические слои радиуса r и бесконечно малой толщины dr. Масса такого слоя dm легко вычисляется:

где - плотность материала цилиндра.

    Рис. 4.4

Подставим это выражение в (4.9) и проведем интегрирование:

.

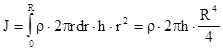Рис.4.5

Последнему соотношению можно придать другой вид, учитывая, что равенство определяет массу m всего цилиндра:

. (4.12)

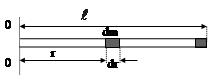
б) В качестве другого примера рассмотрим применение (4.9) для расчета момента инерции тонкого длинного однородного стержня, имеющего сечение S произвольной формы, относительно оси, проходящей через один из его концов перпендикулярно самому стержню (рис. 4.5).

Тонким можно считать стержень, для которого выполняется услови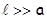е , где 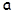определяет величину наибольшего поперечного размера стержня. Разобьем стержень на элементарные участки . Подставив это равенство в (4.9) и проведя интегрирование, получим

или с учетом, что 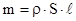, окончательно имеем

(4.13)

Ниже приведем соотношения, определяющие моменты инерции некоторых однородных симметричных тел:

- момент инерции материальной точки относительно произвольной оси:

; (4.14)

- момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню

, (4.15)

где 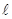- длина стержня;

- момент инерции тонкостенного цилиндра относительно его геометрической оси:

; (4.16)

- момент инерции толстостенного цилиндра относительно его геометрической оси (R₁ и R₂ - радиусы внутренней и внешней поверхностей цилиндра):

(4.17)

Отметим здесь, что результаты (4.12) и (4.16) являются частными по отношению к (4.17). Формула (4.12) получается из (4.17) при R₁=0 и R₂=R. Формула (4.16) получается из (4.17) при R₁=R₂=R;

- момент инерции сплошного шара относительно любой оси, проходящей через его центр

(4.18)

В заключение этого пункта можно сделать вывод, что по крайней мере, для однородных симметричных тел моменты инерции относительно геометрической оси можно представить в виде

, (4.19)

где коэффициент пропорциональности k учитывает характер распределения массы тела относительно оси симметрии, причем значения k заключены в пределах

(4.20)

Отметим, что приведенный выше вывод справедлив, вообще говоря, для моментов инерции относительно оси, проходящей через центр инерции произвольного тела. В этом случае величина R в (4.19) представляет собой некоторый характерный, поперечный оси, размер тела. Доказательство этого факта выходит за рамки данного пособия.

Контрольные вопросы.

4.3. Докажите справедливость соотношений (4.15), (4.17) и (4.18).

Дата добавления: 2014-01-07