Кинетическая энергия вращающегося твердого тела

Поскольку твердое тело представляет собой частный случай системы материальных точек, то кинетическая энергия тела при вращении вокруг неподвижной оси Z будет равна сумме кинетических энергий всех его материальных точек, то есть

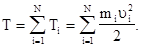
Все материальные точки твердого тела вращаются в этом случае по окружностям с радиусами и с одинаковыми угловыми скоростями 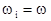. Линейная скорость каждой материальной точки твердого тела равна . Кинетическая энергия твердого тела примет вид

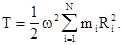
Сумма в правой части этого выражения в соответствии с (4.4) представляет собой момент инерции этого тела относительно данной оси вращения. Поэтому формула для расчета кинетической энергии вращающегося относительно неподвижной оси твердого тела примет окончательный вид:

. (4.21)

Здесь учтено, что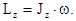

Вычисление кинетической энергии твердого тела в случае произвольного движения значительно усложняется. Рассмотрим плоское движение, когда траектории всех материальных точек тела лежат в параллельных плоскостях. Скорость каждой материальной точки твердого тела, согласно (1.44), представим в виде

,

где в качестве мгновенной оси вращения выберем ось, проходящую через центр инерции тела перпендикулярно плоскости траектории какой-либо точки тела. В этом случае в последнем выражении 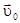представляет собой скорость центра инерции тела, - радиусы окружностей, по которым вращаются точки тела с угловой скоростью вокруг оси, проходящей через центр его инерции. 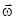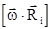Так как при таком движении ^, то вектор, равный , лежит в плоскости траектории точки.

На основании сказанного выше кинетическая энергия тела при его плоском движении равна

.

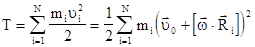Возводя выражение, стоящее в круглых скобках, в квадрат и вынося за знак суммы постоянные для всех точек тела величины, получим

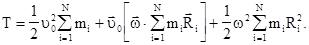(4.22)

Здесь учтено, что ^.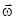

Рассмотрим каждое слагаемое в правой части последнего выражения отдельно. Первое слагаемое в силу очевидного равенства 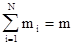равно

.

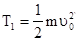Второе слагаемое равно нулю, так как сумма определяет радиус-вектор центра инерции (3.5), который в данном случае лежит на оси вращения. Последнее слагаемое с учетом (4.4) примет вид . Теперь, окончательно, кинетическая энергия при произвольном, но плоском движении твердого тела может быть представлена в виде суммы двух слагаемых:

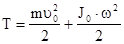, (4.23)

где первое слагаемое представляет собой кинетическую энергию материальной точки с массой, равной массе тела и движущейся со скоростью, которую имеет центр масс тела;

второе слагаемое представляет собой кинетическую энергию тела, вращающегося вокруг оси (движущейся со скоростью 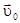), проходящей через его центр инерции.

Выводы: Итак, кинетическая энергия твердого тела при его вращении вокруг неподвижной оси может быть вычислена с помощью одного из соотношений (4.21), а в случае плоского движения с помощью (4.23).

Контрольные вопросы.

4.4. В каких случаях (4.23) переходит в (4.21)?

4.5. Как будет выглядеть формула для кинетической энергии тела при его плоском движении, если мгновенная ось вращения не проходит через центр инерции? Каков при этом смысл входящих в формулу величин?

4.6. Покажите, что работа внутренних сил при вращении твердого тела равна нулю.

Дата добавления: 2014-01-07