
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно большие и бесконечно малые последовательности
|
|
|
|
Определение. Последовательность { 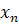 } называется бесконечно большой, если
} называется бесконечно большой, если 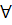 А>0
А>0 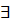 N
N 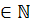 выполняется неравенство
выполняется неравенство 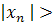 А.
А.
Определение. Последовательность { 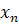 } называется бесконечно малой, если
} называется бесконечно малой, если 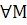 >0
>0 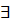 N
N 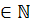 :
:  выполняется
выполняется 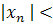 М.
М.
Пример. Используя определение, показать, что последовательность {n} является бесконечно большой.
Решение.
Пусть А>0. Из 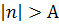 получим, что
получим, что 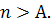 Если взять N≥А, то для всех n>N будет выполняться n>N≥А, т.е. n>А.
Если взять N≥А, то для всех n>N будет выполняться n>N≥А, т.е. n>А.
Теорема. Если { 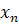 } – бесконечно большая последовательность и все ее члены отличны от 0, то последовательность {
} – бесконечно большая последовательность и все ее члены отличны от 0, то последовательность { 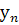 }={
}={  }
}
бесконечно малая, и наоборот, если { 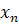 }- бесконечно малая последовательность, то {
}- бесконечно малая последовательность, то { 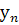 }={
}={  }- бесконечно большая последовательность (при
}- бесконечно большая последовательность (при 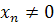

Теорема. Сумма и разность двух бесконечно малых последовательностей есть бесконечно есть бесконечно малые последовательности.
Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Замечание. Частное двух бесконечно малых последовательностей может быть любой последовательностью и может не иметь смысла.
Теорема. Произведение ограниченной последовательности на бесконечно малую, есть бесконечно малая последовательность.
Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 587; Нарушение авторских прав?; Мы поможем в написании вашей работы!