Теорема умножения вероятностей

а) Независимые и зависимые события

Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого.

Пример. Из ящика, в котором 100 деталей, из них 12 нестандартных, берут наудачу одну деталь. Вероятность того, что деталь стандартная, равна 0,88. После возвращения этой детали опять наудачу берут одну деталь; вероятность появления стандартной детали опять будет равна 0,88.

Эти события независимы.

Два события называются зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления другого.

Пример. Если в ранее рассмотренном примере в первом испытании появилась стандартная деталь, то вероятность появления стандартной детали без возвращения взятой в первом испытании равна 87/89.

В этом случае события зависимые.

б) Теорема умножения вероятностей независимых событий

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий

р(АВ) = р(А)р(В). (2.5)

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

Пример. Система состоит из трех последовательно соединенных элементов. Вероятность безотказной работы первого элемента р(А) = 0,9, второго - р(В) = 0,92, третьего - р(С) = 0,95. Определить вероятность безотказной работы системы.

Система будет работать безотказно при совмещении всех событий ABC. р(АВС) = р(А)р(В)р(С) = 0,9x0,92x0,95 = 0,7866.

в) Вероятность появления хотя бы одного события

Теорема. Вероятность появления хотя бы одного из событий А₁, А₂, А_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

;

p(A)=1 - g₁g₂….g_n. (2.6)

Если g₁=g₂=…….=g_n=g, то р(А)=1 - gⁿ.

Пример. Система состоит из n параллельно соединенных элементов (рис. 2.1). Вероятность безотказной работы каждого из элементов равна р. Система продолжает оставаться работоспособной, если не отказал хотя бы один элемент.

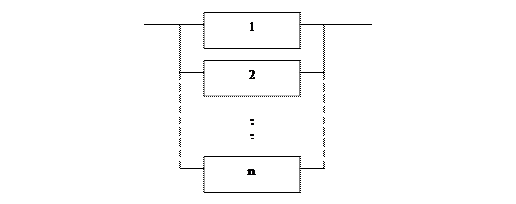
Pиc. 2.1 Системапараллельно-соединенных элементов

Определить вероятность безотказной работы системы.

Дата добавления: 2014-01-07