Основные законы геометрической оптики

Лекция №11

ОПТИКА

Основные законы геометрической оптики. Отражение. Преломление. Призма. Линзы. Формула линзы. Оптические приборы: телескоп, микроскоп, человеческий глаз. Волновая природа света. Дифракция. Интерференция. Поляризация. Принцип Гюйгенса. Электронный микроскоп.

Основной поток света на Землю приходит от Солнца. Поэтому Солнце, как источник тепла и света всегда привлекало человека. Первым врачом, упоминавшим о целебной силе солнечного тепла и света, был Гиппократ[1], а также его последователи Гален[2] и Авиценна[3]. Аристотель[4] первым высказал мысль о том, что свет – нечто, попадающее в глаза. О прямолинейности распространения света писал Евклид[5].

Все попытки понять, что такое свет вплоть до И.Ньютона концентрировались вокруг идеи о корпускулярной природе света.

Во времена Ньютона итальянец Ф.Гримальди заметил, что свет проникает в область геометрической тени. Впоследствии это явление получило название дифракции. Английский физик Р.Гук исследовал другое явление, получившее впоследствии название интерференции. Изучая образование цветных колец на тонких пленках, а также теорию упругости, он высказал предположение, что свет состоит из быстрых колебаний среды. Следом за ним голландский физик Х.Гюйгенс создал математическую волновую теорию света. Между Р.Гуком и Ньютоном разгорелся спор о природе света. Лишь сто лет спустя физики вернулись к волновой теории света в работах Т.Юнга и О.Френеля. На ее основе они смогли объяснить отражение, дифракцию и интерференцию света.

В современной физике описанием, трактовкой, предсказанием явлений, связанных с формированием зрительных образов у человека, занимается раздел физики, называемый оптикой. В оптике в качестве источника света рассматриваются, как непосредственные источники света (Солнце, свеча, лампа накаливания, лазер), так и объекты, отражающие его (Луна, планеты, зеркала, освещенные здания и т.д.).

Как показало дальнейшее развитие физики, правы были оба великих физика. Поэтому в настоящее приняты два подхода к описанию оптических явлений. Свет – как луч. Этот подход изучается в геометрической оптике. Свет - как волна. В этом случае явления описываются в рамках волновой теории света.

Наблюдения за распространением света во многих случаях свидетельствуют о том, что свет распространяется прямолинейно. Это и тень от предмета, освещаемого уличным фонарем, и движение тени Луны по Земле во время солнечных затмений, и лазерная юстировка приборов, и многие другие факты. Во всех случаях мы подразумеваем, что свет движется по прямой линии.

В геометрической оптике рассматриваются законы распространения света в прозрачных средах на основе представления о свете как о совокупности световых лучей – прямых или искривленных линий, которые начинаются на источнике света и продолжаются бесконечно. Если среда однородная, то лучи распространяются по прямым линиям. Эта закономерность известна как закон прямолинейного распространения света. Прямолинейность распространения света проявляется в образовании тени от непрозрачного тела, если его освещают точечным источником света. Если тот же предмет освещают двумя точечными источниками света S ₁ и S ₂ (рис.11.1) или одним протяженным источником, то на экране возникают участки, которые освещены частично и носят название полутени. Примером образования тени и полутени в природе является солнечное затмение. Область применения этого закона ограничена. При малых размерах отверстия, через которое проходит свет (порядка 10^-5м), как уже отмечалось выше, наблюдается явление отклонения света от прямой траектории, которое получило название дифракции света.

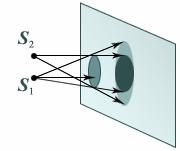
Рис.11.1. Образование тени и полутени..

В неоднородной среде лучи распространяются по криволинейным траекториям. Примеров неоднородной среды – разогретый песок в пустыне. Вблизи него воздух имеет высокую температуру, которая с высотой уменьшается. Соответственно плотность воздуха ближе к поверхности пустыни уменьшается. Поэтому лучи, идущие от реального объекта, преломляются в слоях воздуха, имеющих различную температуру, и искривляются. Как результат – формируется ложное представление о местоположении объекта. Возникает мираж, то есть изображение вблизи поверхности может казаться расположенным высоко на небе. По сути, это явление аналогично преломлению света в воде. Например, конец шеста, опущенного в воду, нам будет казаться расположенным ближе к ее поверхности, чем на самом деле.

Другой закон геометрической оптики - закон независимости световых пучков означает, что эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки. Таким образом, пучки света можно складывать и расщеплять. Сложенные пучки будут ярче. Хорошо известный пример из истории сложения пучков солнечного света, когда при защите города от нападения вражеских судов с моря пучки света от Солнца множеством зеркал направлялись на судно в одну точку, так что в жаркое лето на деревянном судне возникал пожар. Многие из нас в детстве с помощью увеличительного стекла, собирающего свет, пробовали выжигать буквы на деревянной поверхности.

Третий факт, установленный экспериментально, - скорость света постоянна. Ее впервые измерил датский астроном Ремер[6] в 1675 году. Наблюдая затмение спутника Юпитера, Ио, он заметил, что когда Земля находится по отношению к Юпитеру соответственно в ближней и дальней точках своей орбиты (расстояние до Юпитера различается на диаметр орбиты Земли). Время нахождения спутника Юпитера в его тени оказывалось различным. Появление из тени Юпитера его спутника отличалось на 22 минуты (рис.11.2).

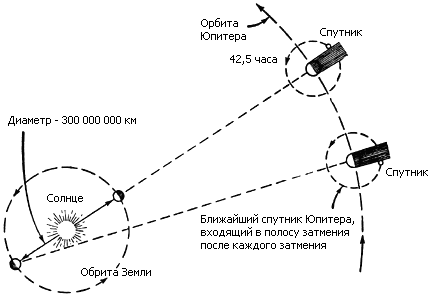
Рис. 11.2. Опыт Ремера по измерению скорости света.

Он понял, что этот факт обусловлен конечностью скорости света, которую он вычислил, разделив диаметр земной орбиты на 22 мин. Скорость света составила 215000 км/с. В 1849 году французский физик Физо[7] и в 1881 году американский физик Майкельсон[8] повторили опыты по измерению скорости света и существенно уточнили значение скорости света. Опыт Майкельсона заключался в быстром вращении восьмигранника. Если свет за 1/8 его оборота успевал долететь до горы и, отразившись там от зеркала, вернуться так, что плоскость восьмигранника симметрично отразит свет в противоположном направлении, то наблюдатель сможет увидеть его (рис.11.3). По скорости вращения восьмигранника, зная расстояние до горы, где свет отражался от зеркала можно вычислить его скорость.

В этом эксперименте Майкельсон получил значение скорости света с=(299796 ± 4) км/с. Современное значение скорости света составляет:

с=(299792456.2 ± 0.8) м/с. (11.1.1)

Скорость света в различных средах разная. Причем, чем выше плотность среды, тем меньше в ней скорость распространения света:

, (11.1.2)

где n – показатель преломления среды.

Отражение света в плоском зеркале. Свет, падая на поверхность какого-либо предмета, частично отражается, а другая часть света либо поглощается предметом, если он не прозрачен, либо преломляется и проходит сквозь него, если предмет прозрачен. По отраженному от предмета свету (которому соответствует конкретная его длина волны) мы ощущаем цвет предмета. Абсолютно черное тело поглощает практически все лучи света, а посеребренный предмет отражает более 95% света.

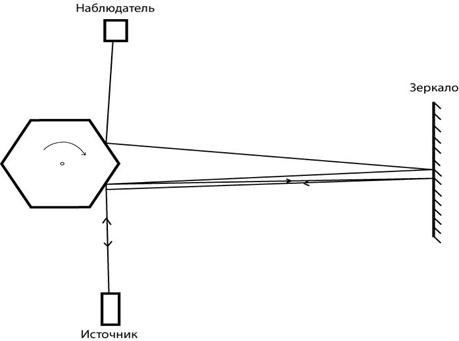
Рис. 11.3. Опыт Майкельсона по измерению скорости света. Восьмигранник!!!

Различают зеркальное и диффузионное отражение света. Зеркальным называют отражение света, когда падающий параллельный пучок света сохраняет свою параллельность после отражения.

Если размеры неровностей поверхности больше длины волны падающего света, то он рассеивается по всевозможным направлениям, такое отражение света называют рассеянным или диффузионным.

Законы зеркального отражения (рис.11.4а) были известны еще древним грекам. Они формулируются так:

1. Отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения.

2. Угол падения равен углу отражения:

(11.1.3)

Пример 11.1. На рис.11.4б приведен пример отражения лампочки в зеркале, когда возникает так называемое ее мнимое изображение. Два луча А и Б по описанным выше правилам отражаются от зеркала, то есть угол падения равен углу отражения. Причем оба луча, падающие на зеркало лежат в одной плоскости. В принципе таких лучей можно провести любое количество, но нам важно найти их точку пересечения. Для этой цели достаточно двух лучей. Как видно в точке пересекаются не сами лучи, а их продолжения. Поэтому изображение называют мнимым.

а)

б)

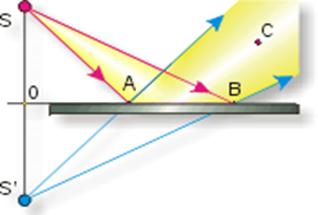Рис.11.4. Законы отражения света (а), и отражение лампочки в плоском зеркале (б).

Пример 11.2. Рассмотрим более сложный пример (рис.11.5). Два зеркала, расположенных друг относительно друга под углом 90⁰, причем лампочка расположена на одинаковом расстоянии от каждого из зеркал. По аналогии с предыдущим примером лампочка отразится в каждом из двух зеркал (относительно 1-ой плоскости и относительно 2-ой плоскости). Однако возникнет еще одно мнимое изображение лампочки, поскольку мнимое изображение, например, относительно 1-ой плоскости зеркально отразится во второй плоскости.

Изображение лампочки в каждом из зеркал примера 11.1 называется мнимым, поскольку в действительности лучи не сходятся в изображении, а сходятся их продолжения за зеркалом в мнимое изображение лампочки.Таким образом, возникнет не два, как ожидается на первый взгляд, а три мнимых изображения лампочки.

Известно из истории, что в древние времена системы плоских зеркала применялись для поджигания кораблей противника. При этом большое число зеркал направлялось в одну точку, пучки солнечного света складывались и нагревали поверхности деревянных конструкций кораблей до температуры возгорания дерева.

Изображения в сферических зеркалах. Отражающие поверхности могут иметь не плоскую форму, чаще всего она представляет собой сегмент сферы. Сферическим зеркалом называют поверхность шарового сегмента, зеркально отражающую свет. Сферические зеркала бывают выпуклые и вогнутые. Сферическое зеркало называется выпуклым, если отражение происходит от внешней стороны поверхности сферического сегмента, т.е. если центр зеркала находится к источнику света ближе, чем края зеркала. Сферическое зеркало называется вогнутым, если отражающей поверхностью служит внутренняя сторона сферического сегмента, т.е. если центр зеркала находится дальше от источника света.

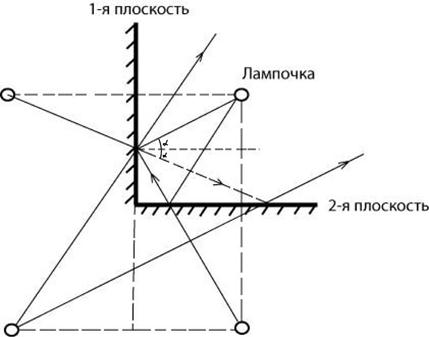
Рис. 11.5. К объяснению отражения лампочки в примере 11.2.

Для каждого из параллельных лучей, падающих на вогнутое зеркало, в точке их падения выполняются оба закона отражения. Если размеры сферического зеркала малы по сравнению с его радиусом кривизны, так что лучи отражаются от него под малым углом, то они пересекутся в точке, которая называется фокусом зеркала (точка F на рис.11.6). Центром зеркала называют точку, которая расположена на одинаковом расстоянии от краев зеркала (А на рис.11.6). Расстояние АС представляет собой радиус кривизны зеркала R, а точка 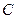называется центром кривизны зеркала. Расстояние между фокусом и центром зеркала AF называется фокусным расстоянием зеркала F:

, (11.1.4)

где R – радиус кривизны зеркала. На рис.11.6 видно, что фокусное расстояние равно половине радиуса R. Это следует из того, что FA=FB, а треугольник FCB равнобедренный, то есть FC=FB.

Главная ось зеркала определяется как прямая, проходящая через фокус и центр сферического зеркала (на рис.11.6 прямая АС). Луч, направленный вдоль главной оси зеркала, отражаясь, движется по тому же пути в обратном направлении.

Плоскость, проходящую через главный фокус зеркала, расположенный на главной оси, перпендикулярно ей, называют фокальной плоскостью.

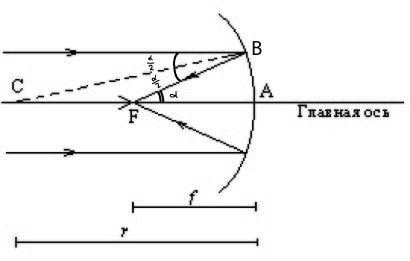
Рис.11.6. Вогнутое зеркало.

Формула сферического зеркала. Вывод формулы сферического зеркала аналогичен выводу формулы линзы, которые будут обсуждаться ниже. Поэтому приведем лишь конечный результат вывода.

Для вогнутого сферического зеркала радиуса R и предмета, расположенного на расстоянии d от центра зеркала, изображение будет располагаться на расстоянии f от центра зеркала, которое определяется по формуле:

, (11.1.5)

или:

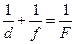. (11.1.6)

Аналогично для выпуклого зеркала формула (11.1.6) отличается только знаком у фокусного расстояния. Это обусловлено тем, что после рассеяния на поверхности выпуклого зеркала лучи будут расходиться. Сходиться будут их продолжения за зеркалом. Поэтому кривизна зеркала считается отрицательной:

. (11.1.7)

Величину, обратную фокусному расстоянию F сферического зеркала, называют его оптической силой D линзы:

. (11.1.8)

Отношение расстояний от центра зеркала до изображения и до предмета равно отношению размеров изображения Н и предмета h, рассматриваемого в сферическое зеркало:

(11.1.9)

Величина Г называется увеличением (уменьшением) зеркала.

На рис.11.7 приводятся построения изображений предмета в вогнутом зеркале в случаях, когда предмет располагается ближе и дальше фокусного расстояния (рис.11.7а и рис.11.7б), а также в выпуклом зеркале (рис.11.7в). Правила построения достаточно простые:

- луч, проходящий через фокус зеркала, после отражения становится параллельным и наоборот;

- угол падания луча равен углу его отражения;

- если луч, параллельный главной оси зеркала, падает на выпуклую поверхность, то через главный фокус зеркала проходит продолжение луча;

- луч, проходящий через центр сферической поверхности, после отражения от зеркала возвращается по тому же пути (поэтому рассматриваемая точка 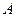, центр кривизны зеркала 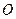, и изображение точки 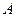- точка лежат на одной линии).

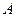На рис.11.7а изображение представляет собой пересечение двух лучей. Первый идет параллельно главной оптической оси, и после отражения от зеркала проходит через его главный фокус . Второй луч из точки проходит через фокус зеркала , и, отражаясь от зеркала, идет параллельно главной оптической оси. Точкапредставляет собой пересечение двух описанных лучей. Точку пересечения можно получить, направив луч в центр зеркала 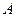, и построив угол отраженного луча, равный углу падающего луча. Однако такой способ используется при построении изображений редко, так как достаточно первых двух лучей.

На рис11.7б, когда источник света располагается ближе к зеркалу, чем его фокус . Первый луч их точки А соединяется с центром кривизны зеркала О. По правилам построения изображений он должен пройти через точку . Второй луч движется параллельно главной оси зеркала. Он проходит через фокус зеркала, его продолжение через точку . Положение конца вектора – точки получается пересечением этих двух лучей. Похожим образом можно построить изображение в третьем случае. Луч из точки 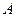проводится параллельно главной оптической оси. Точка пересечения с поверхностью зеркала соединяется с главным фокусом. Вторая линия соединяет точку 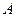с центром кривизны зеркала 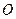. Пересечение первой и второй линии происходит в точке .

Таким образом, вогнутое зеркало на практике действует как увеличительное стекло. Их применяют, как линзы в телескопах, биноклях. Хорошо известно, что таким зеркалом пользуются при осмотре больных отоларингологи, офтальмологи. Хорошо известно, что если лампочка карманного фонарика оказывается в фокусе зеркала отражателя, то луч света практически не расширяется с расстоянием, и мы можем осветить далекие предметы. Так работают и фары автомобиля, и прожектор.

Для того, чтобы изображение было четким, лучи должны сходиться в одной точке. Сферическое зеркало не создает такого четкого изображения, как и плоское зеркало, так как свет разной длины волны отражается от зеркала под различными углами.

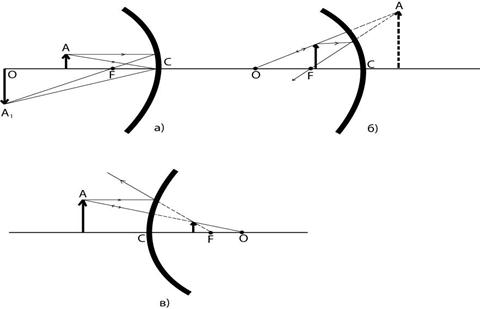
Рис. 11.7. Построение изображения предмета в вогнутом (а) и (б) и выпуклом (в) зеркалах. а) – ошибка!!!

Поскольку утверждение о том, что все лучи проходят через точку, выполняется лишь приближенно, то чем больше размеры зеркала, тем хуже приближение и тем более расплывчатым оказывается изображение. Этот «дефект» сферических зеркал называется сферической аберрацией.

Преломление света. Экспериментально были установлены законы преломления света:

1. Падающий и преломленный луч лежат в одной плоскости с перпендикуляром, проведенным к границе раздела двух сред в точке падения луча.

2. Произведение синуса угла падения луча на показатель преломления данной среды является постоянной величиной, или выполняется соотношение:

(11.1.10)

Если имеется не одна, а несколько плоскослоистых сред с различными показателями преломления, то, рассматривая преломление луча на каждой из границ, мы видим, что закон преломления имеет форму закона сохранения величины 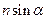. Закон преломления установлен В. Снеллиусом[9]. Величину n называют относительным показателем преломления.

Показатель преломления относительно вакуума называют абсолютным показателем преломления. Это следует, если в формуле (11.1.10) показатель преломления вакуума считать равным единице n₁ =1.

По физическому смыслу луч перпендикулярен фронту волны. Скорость его распространения в воздухе или вакууме равна скорости света 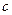, а в более плотной среде она меньше скорости света и составляет 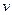. Показатель преломления n равен отношению скорости света в вакууме к его скорости v в среде:

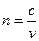(11.1.11) После попадания луча на границу раздела двух сред – он делится на две части (рис.11.8). Одна часть отражается по законам отражения от плоского зеркала, а другая проходит в среду под углом, определяемым законом преломления света.

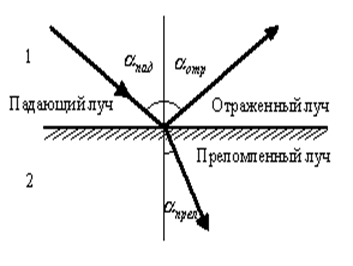Рис.11.8. К определению закона преломления света.

Полное внутреннее отражение. При распространении света из оптически более плотной среды в менее плотную среду, угол преломления будет больше угла падения. При некотором угле падения луча, угол преломления луча будет стремиться к 90⁰ (рис.11.9).

Рис. 11.9. Полное отражение.

В этом случае формула (11.1.10) представима в виде:

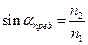(11.1.12)

Угол падения, при котором угол преломления равен прямому углу, называется критическим углом падения.

Если угол падения больше критического, то преломленный луч отсутствует, и все падающие лучи полностью отражаются от границы раздела.

На явлении полного внутреннего отражения строится волоконная оптика (рис.11.11). Для того, чтобы весь свет проходил по волокну, диаметр волокон, как отмечалось выше, должен быть очень маленьким. Иначе часть светового пучка в результате преломления будет уходить наружу, и интенсивность светового потока будет уменьшаться. Диаметр волокон составляет микроны, а пучок таких волокон, который содержит от десятков до тысяч волокон, называют световодом. Принцип работы оптоволоконной оптики заключается в том, что луч, проходящий в ней, как видно на рис.11.10 постоянно испытывает полное внутреннее отражение. Световод можно изгибать, а лучи при этом все равно полностью отражаются от поверхности раздела двух сред.

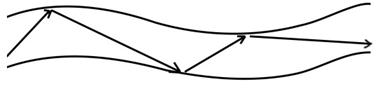
Рис. 11.10. Волоконная оптика.

На этом принципе основан медицинский прибор эндоскоп. Этот прибор позволяет осматривать внутренние органы человека. Пучок волокон подводит свет к внутренним органам, который отражаясь от поверхности, по другой части волокон возвращается назад. Таким способом можно осматривать, например, желудок, пищевод, бронхи, носоглотку и другие органы без хирургического вмешательства.

Световоды лежат в основе действия приборов лазерной терапии крови (например, МУСТАНГ, МАТРИКС). Световод диаметром 500 мкм и длиной 20 см подключается одним концом к лазеру, а другим вводится через иглу в кровеносные сосуды. Освещение лазерным излучением крови позволяет осуществить ее чистку. Эта процедура в настоящее время широко используется в современных кардиологических центрах и санаториях.

Оптоволоконные линии прокладываются для приведения как обычной, так и компьютерной связи.

Призма. Монохроматический свет в треугольной стеклянной призме проходит через преломляющие грани призмы АВ и АС (рис.11.11). Угол между ними называется преломляющим углом призмы. Если плотность вещества призмы больше, чем плотность окружающей среды, то выходящий из нее луч отклоняется к основанию призмы. Луч в призме отклоняется на угол δ, который связан с углами падения луча на призму и выхода из нее соответственно α₁ и α₂.

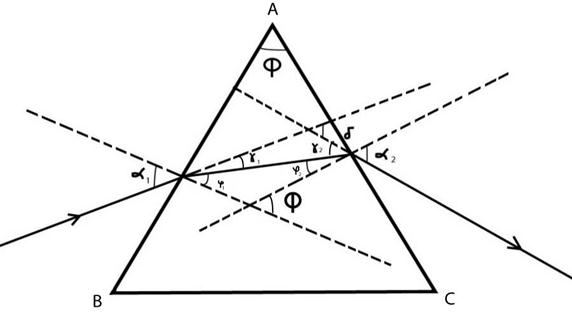
Рис. 11.11. Связь угла преломления и отклонения луча.

Как видно на рис.11.11:

(11.1.13)

, (11.1.14)

а угол отклонения луча δ и преломления призмы согласно рис.11.11 определяются соотношениями:

, (11.1.15)

. (11.1.16)

Решая систему уравнений (11.1.13) - (11.1.16) получаем связь между углами падения и выхода луча из призмы с углами преломления призмы и отклонения луча от первоначального направления:

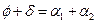(11.1.17)

Учитывая, что для малых углов: ,

Выражение (11.1.17) представим в виде:

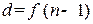(11.1.18)

Призмы используются в конструкциях многих оптических приборов, например, телескопов, биноклей, перископов, спектрометров.

Используя призму, И.Ньютон впервые разложил свет на составляющие, и увидел, что на выходе из призмы возникает разноцветный спектр, причем цвета расположены в том же порядке, как и в радуге. Оказалось, что естественный «белый» свет состоит из большого количества разноцветных пучков.

Дата добавления: 2014-01-07