Оптические приборы

Линзы

На практике линзы играют ту же роль, как и сферические зеркала. Понятия определения и законы распространения света для линз действуют те же, что и для сферических зеркал.

Линзой[10] называют прозрачное для света тело, ограниченное двумя поверхностями, одна из которых обычно сферическая, (иногда цилиндрическая), а вторая – сферическая или плоская. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т.д.

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Линза называется выпуклой, если ее середина толще, чем края, и вогнутой, если середина линзы тоньше, чем края. На рис.11.12 показаны различные виды линз: двояковыпуклые (1), плосковыпуклые (2), двояковогнутые (3), плосковогнутые (4), выпукло - вогнутые (5), вогнуто - выпуклые (6).

Характеристики линз и правила построения изображений в них мало отличаются от рассмотренных выше правил для сферических зеркал.

Главной оптической осью линзы называется прямая, проходящая через центры кривизны поверхностей линзы.

Главным фокусом линзы называется точка на главной оптической оси, в которой пересекаются лучи светового пучка, распространяющиеся параллельно главной оптической оси (рис.11.13а).

Фокусное расстояние – это расстояние между оптическим центром линзы и ее фокусом (рис.11.13а).

Оптическим центром линзы называется точка на главной оптической оси, через которую все световые лучи проходят, не изменяя направления, то есть не преломляясь (рис.11.13а).

Плоскости, проходящие через главные фокусы линзы, перпендикулярно ее главной оптической оси называют фокальными плоскостями (рис.11.13б).

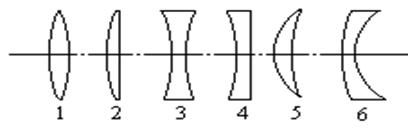
Рис. 11.12. Виды линз: двояковыпуклые (1); плосковыпуклые (2); двояковогнутые (3); плосковогнутые (4); выпукловогнутые (5); вогнутовыпуклые (6)

Побочной оптической осью называют любую прямую, проходящую через оптический центр линзы и не совпадающую с главной оптической осью. В этом случае лучи, двигающиеся параллельно побочной оптической оси, собираются на фокальной плоскости линзы (рис.11.13б), а фокус расположен на пересечении побочной оптической оси с фокальной плоскостью.

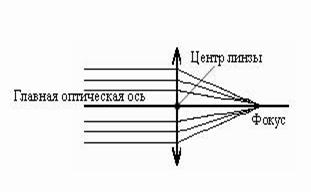
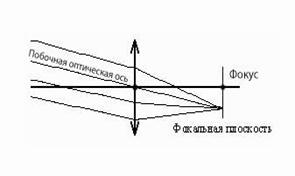
а) б)

Рис.11.13. Характеристики линзы: фокус (а), фокальная плоскость (б), главная и побочная оптическая оси, центр линзы.

Правила построения изображения в линзах. Для построения изображения точки или отрезка в различных линзах используют правила, основанные на данных выше определениях:

1. Луч, проходящий через оптический центр линз, не изменяет своего направления.

2. Луч, идущий параллельно главной оптической оси, после преломления пройдет через фокус линзы.

3. Луч (или его продолжение), проходящий через фокус линзы, после преломления в ней выходит из линзы параллельно ее главной оптической оси.

4. Луч, движущийся параллельно побочной оптической оси собирается в точку, расположенную на фокальной плоскости.

Рассмотрим примеры построения изображения в собирающей линзе.

Пример 11.3. Объект расположен на расстоянии, большем, чем фокусное расстояние выпуклой линзы (рис.11.14а). Из верхней точки вектора слева от линзы выходят два луча. Один луч, не преломляясь, проходит через центр линзы. Необходимо отметить, что во всех случаях построения изображений в линзах, конец вектора источника света, его изображения и центра линзы лежат на одной прямой. Второй луч движется параллельно главной оптической оси, и, преломляясь в ней, проходит через главный фокус линзы. Справа от линзы два этих луча вновь пересекаются, образуя нижнюю точку перевернутого изображения исходного вектора. Луч из нижней точки вектора, движется через центр линзы, не преломляясь. Изображение вектора получается при опускании перпендикуляра на главную оптическую ось линзы.

Пример 11.4. Объект расположен на расстоянии, меньшем, чем фокусное расстояние выпуклой линзы (рис.11.14б). В этом случае, как и в предыдущем примере, один луч из верхнего конца вектора движется параллельно главной оптической и, преломляясь в ней, проходит через главный фокус линзы. Второй не преломляясь, проходит центр линзы. За линзой лучи расходятся, а перед ней пересекаются при продолжении в обратную сторону лучей, проходящих через центр линзы и его главный фокус. В этом случае возникает мнимое увеличенное изображение предмета.

Пример 11.5. Объект расположен на расстоянии, большем, чем фокусное расстояние вогнутой линзы (рис.11.14в). Построение в этом примере отличается тем, луч от верхнего конца вектора, движущийся параллельно главной оптической, после прохождения линзы отклоняется в другую сторону от главной оптической оси. Второй луч от верхней точки вектора проходит через центр линзы. На этом луче расположится и изображение верхнего конца вектора. Со вторым лучом пересекается продолжение этого луча. Изображение, как и в предыдущем примере, оказывается мнимым, но уменьшенным.

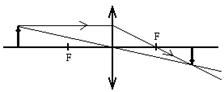
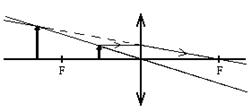
а) б)

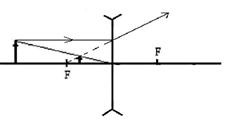в)

Рис. 11.14. Построение изображения в линзах: а) - изображение действительное перевернутое; б) - изображение мнимое прямое, в) – мнимое прямое изображение, получаемое в вогнутых линзах.

Формула линзы. Выведем формулу линзы для простейшего случая, когда она считается тонкой и двояковыпуклой, как на рис.11.14а. Все обозначения представлены на рис.11.15. Фокусное расстояние линзы равно F, расстояние от предмета высотой H до линзы составляет d. Соответственно расстояние до изображения предмета и его размер составляют f и h.

Составим систему уравнений для вывода формулы линзы. Для этого рассмотрим подобные треугольник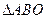и и 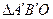, из которых следует:

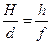(11.2.3)

Аналогично из подобных треугольников 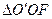и 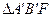следует:

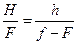(11.2.4)

Решая систему уравнений (11.2.3) и (11.2.4) делением первого уравнения на второе получаем:

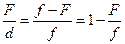
Откуда получаем формулу линзы:

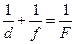(11.2.5)

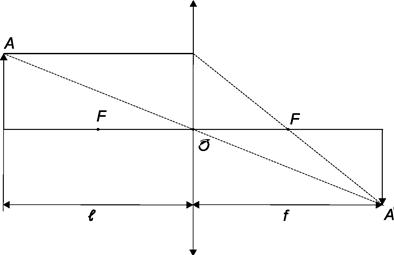
Рис.11.15. К выводу формулы линзы.

В общем виде для выпуклых и вогнутых тонких линз, а также при построении мнимых изображений формула линзы приобретает вид:

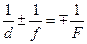(11.2.6)

Так в случае прямого мнимого изображения на рис.11.14б формула линзы записывается так:

,

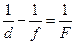а в случае мнимого прямого изображения, получаемого в вогнутой линзе, формула линзы (рис.11.14в) имеет вид:

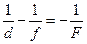
Если учитывать второй радиус кривизны линзы, то формула линзы приобретает вид:

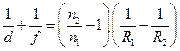(11.2.7)

где фокусное расстояние линзы определяется соотношением:

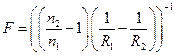(11.2.8)

Линзы очень широко используются в медицине и промышленности. Они лежат в основе конструкции телескопов, биноклей, фотоаппаратов, проекционной техники, микроскопов. Обыденным стало изготовление очков, в которых ходят миллиарды людей на земле. Это лишь малая часть примеров использования оптики.

Конструирование любой оптической техники, состоящей из двух и более линз, построено на расчетах по формуле линзы. При этом изображение, полученное в первой линзе, рассматривается второй линзой как исходное положение предмета, считая, что первой линзы не было вообще. Получается второе изображение, которое может рассматриваться последовательно третьей линзой, затем четвертой линзой рассматривается изображение в третьей линзе, и так далее. Число линз не меняет принцип независимого рассмотрения изображения как первичного положения объекта. В каждой линзе рассматривается изображение, полученное в предыдущей линзе независимо от числа линз. Так обычно оконное стекло можно представить в виде большого количества тонких линз разного типа. А результат последовательного сложения всех изображений в нем тот, что мы видим в окно.

Телескопы. Первый телескоп был изобретен не Галилеем[11], как обычно пишут в литературе, а в Голландии в 1604 году или в Италии в 1590 году. Первое описание телескопа Галилея и Кеплера было дано Кеплером. Труба Галилея состоит из выпуклой линзы – объектива и вогнутой линзы с малым фокусным расстоянием – окуляра. Изображение в таком телескопе прямое. В телескопе Кеплера в качестве объектива использовалась двояковыпуклая линза, что приводило к перевернутому изображению предметов. Телескоп – прибор, состоящий из двух и более линз, который применяется для увеличения объектов, находящихся на очень большом удалении. В большинстве случаев объект можно считать расположенным на бесконечности.

Телескоп Кеплера имеет две собирающие линзы, расположенные на противоположных концах длинной трубы (рис.11.17а). Линза, обращенная к объекту, называется объективом. Она создает действительное изображение объекта в своей фокальной точке (или вблизи нее, если объект оказывается не бесконечно удаленным). Хотя изображение меньше самого объекта, оно расположено очень близко ко второй линзе, называемой окуляром и действующей как лупа. Это означает, что окуляр увеличивает создаваемое объективом изображение, в результате чего возникает второе, сильно увеличенное изображение, которое будет мнимым. В телескопе Галилея (рис.11.17б) объектив – выпуклая линза и изображение в ней действительное. Он рассматривается окуляром - двояковогнутой линзой.

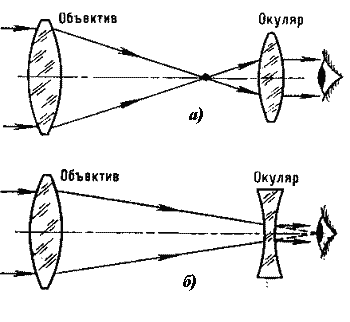
Рис.11.16. ход лучей в телескопе Галилея (а) и Кеплера (б).

Микроскоп. Подобно телескопу, микроскоп (рис.11.18) имеет и объектив, и окуляр. Изобрели первый микроскоп в 1590 голландский мастер очков Ханс Янсен и его сын Захарий Янсен.

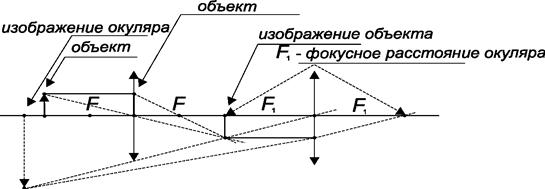
Рис. 11.17. Принципиальная схема микроскопа.

Однако, принципиальная схема микроскопа (рис.11.17) отличается от схемы телескопа, так как микроскоп предназначен для наблюдения очень близких объектов, т.е. расстояние до объекта в микроскопе мало. Объектив микроскопа имеет небольшое фокусное расстояние. Объект расположен перед объективом, вблизи его фокуса. Создаваемое объективом действительное изображение находится за линзой перед окуляром. Расстояние от него до окуляра меньше фокусного расстояния окуляра. Изображение в короткофокусном окуляре строится по схеме, представленной на рис.11.14б. Как видно на рис.11.14 оно оказывается мнимым. Фокусные расстояния подбираются таким образом, чтобы достигнуть максимального увеличения. Под увеличением линзы 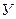понимают отношение углов 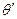и 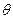, под которыми соответственно виден предмет через линзу и без нее на расстоянии лучшего зрения :

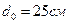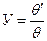
Увеличение микроскопа определяется увеличением его объектива 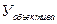и окуляра 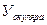и определяется с высокой точностью их произведением:

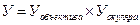
Микроскоп быстро после своего создания стал одним из основных исследовательских инструментов химиков, биологов и медиков.

Человеческий глаз. Человеческий глаз представляет собой замкнутый объем, в который свет попадает через линзу (рис.11.18). Линза глаза (хрусталик) слабо преломляет световые лучи. Плотность хрусталика составляет примерно 1.4 г/см³. Хрусталик обеспечивает тонкую фокусировку глаза. Эта фокусировка достигается сокращением цилиарных мышц, в результате которого происходит изменение кривизны хрусталика и, следовательно, его фокусного расстояния. Способность глаза приспосабливаться к изменению расстояния до предмета называют аккомодацией.

а) б)

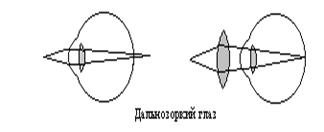
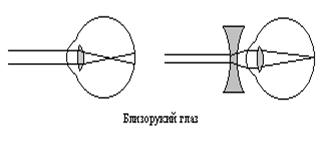
Рис. 11.18. Глаз: дефекты близорукости (а) и дальнозоркости (б)

Офтальмологи характеризуют линзу не фокусным расстоянием, а оптической силой линзы:

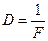(11.3.1)

Оптическая сила линзы измеряется в диоптриях: 1 дптр =1 м^—1. Поскольку фокусное расстояние линзы может иметь разный знак, оптическая сила собирающей линзы является положительной величиной, а рассеивающей - отрицательной.

Два наиболее распространенных дефекта зрения – это близорукость и дальнозоркость. Близорукостью, или миопией, страдает глаз, который может фокусироваться только на близкие объекты. Обычно близорукость обусловлена продолговатым глазным яблоком, но иногда ее причиной бывает чрезмерная кривизна роговицы. И в том и в другом случае изображения далеких предметов фокусируются перед сетчаткой. Используя рассеивающую линзу, которая заставляет параллельные лучи расходиться, можно сфокусировать изображение на сетчатке и тем самым исправить дефект (рис.11.18а). Дальнозоркостью, или гиперопией, страдает глаз, который не может фокусироваться на близких объектах. Указанный дефект возникает при слишком коротком глазном яблоке и (реже) при недостаточной кривизне роговицы. Как видно из рис.11.18б, для коррекции дальнозоркости применяют собирающие линзы.

Астигматизм обычно связан с несферичностью роговицы или хрусталика, вследствие чего изображение точечного объекта имеет вид короткой линии. В сферическую роговицу как бы вложен цилиндрический участок. Как показано на рис.11.19а, цилиндрическая линза превращает точку в отрезок прямой, перпендикулярный оптической оси линзы. Глаз, страдающий астигматизмом, например, в вертикальной плоскости, собирает лучи на меньшем расстоянии, чем в горизонтальной плоскости. Астигматизм исправляют с помощью цилиндрической линзы. Если человек страдает астигматизмом, то для него линзы шлифуют в виде комбинации цилиндрических и сферических поверхностей.

Аберрации. Для малых углов все лучи, выходящие из одной точки объекта, собираются линзой в одной точке, служащей ее изображением. Этот результат основан на приближении для малых углов, когда: 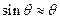. В реальности размеры линз не являются малыми, а отклонения лучей от главной оптической оси происходит на значительные углы. В этом случае изображение точки также оказывается размытым. Это явление носит название аберрации линзы. Аберрации бывают сферические и хроматические.

Если расходящийся пучок света падает на линзу, то параксиальные лучи после преломления пересекаются в точке М (на расстоянии ОМ от оптического центра линзы), а лучи, более удаленные от оптической оси, - в точке N, ближе к линзе (рис.11.19б). В результате изображение светящейся точки на экране, перпендикулярном оптической оси, имеет вид расплывчатого пятна. Такие аберрации называют сферическими. Хроматическими аберрациями называют аберрации, связанные с зависимостью показателя преломления от длины волны. В этом случае точка превращается в набор концентрических цветных окружностей. Избавляются от нее склеиванием двух линз вогнутой и выпуклой, сделанных из стекла с разным показателем преломления.

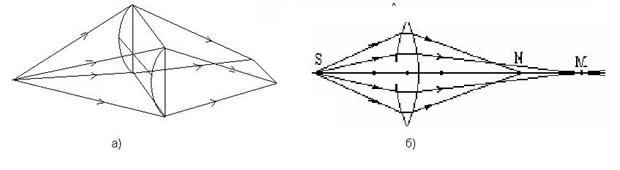
Рис. 11.19. К объяснению возникновения астигматизма (а) и сферической аберрации (б).

Дата добавления: 2014-01-07